объединения двух частей по точкам а и а, & и с и с и т. д. (рис. 5.5.11).

Очевидно, что, за исключением частично заполненной верхней строки на рис. 5.5.11, б, остальная часть рис. 5.5.11, б является диаграммой сортировки для т ключей. По предположению индукции m элементов второй строки этой диаграммы упорядочиваются не более, чем за т шагов. Считая верхнюю строку еще одним шагом, получим, . что первоначальные m+l ключей упорядочиваются не более, чем за т+1 шагов.

Заметим, что алгоритм PARSORT требует только постоянного числа операций с для параллельного выполнения шагов 1 и 2. Таким образом, алгоритм упорядочивает ключи в реальном времени, т. е. за 0(«) шагов по времени, производя на каждом шаге п/2 сравнений. Следовательно, он требует всего О(п) сравнений.

Компромиссы сложности параллельных вычислений

На примере алгоритма SOLLIN мы видели, что параллельные вы-чирления позволяют увеличить скорость работы алгоритма с 0(Л4) до 0(M log2M).Mbi убедились, что наилучшие алгоритмы последовательной сортировки требуют 0(М loggM), а алгоритм PARSORT - 0(М). В литературе имеется достаточно свидетельств того, что, грубо говоря, можно получить выигрыш на порядок величины, если реализовать алгоритм в параллельной модификации. Это утверждение содержится в так называемой гипотезе Минского: параллельные машины, выполняющие последовательную программу над п множествами данных, повышают производительность по крайней мере на множитель O(logn).

Хотя гипотезе Минского найдено несколько контрпримеров, в достаточно большом числе случаев она, по-видимому, дает удовлетворительную оценку повышения скорости вычислений.

Такое повышение скорости не дается бесплатно. Платой оказывается добавление п процессоров, увеличение на порядок величины числа выполняемых операций и, возможно, довольно низкий коэффициент использования процессоров. Вообще говоря, по-видимому, трудно занять все процессоры работой на все время.

Упражнения 5.5

5.5.1. Воспользуйтесь (вручную) алгоритмом SOLLIN для отыскания остовного дерева минимального веса в сети на рис. 5.5.12.

5.5.2. Примените алгоритм PARSORT для упорядочения (вручную) последовательности

12 4 8 И 7 5 6 2 9 3 1 10

*5.5.3. Операции над множествами и арифметические операции. Какие операции над множествами и арифметические операции, по вашему мнению, особенно просто реализовать в виде параллельных алгоритмов? Какие, как вам кажется, особенно трудно запараллелить?

Б.5.4. Напишите простую программу, использующую одну или более параллельных языковых конструкций, описанных в этом разделе.

*5.5.5. Покажите, что всегда можно занумеровать вершины произвольной сети так, чтобы алгоритм SOLLIN нашел остовное дерево минимального веса за один параллельный шаг. Имеет ли этот факт какое-нибудь практическое значение?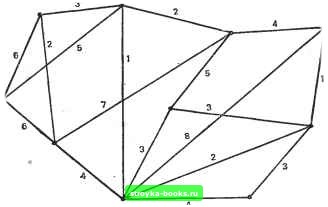

Рис. 5.5.12. Найдите остовное дерево минимального веса с помощью алгоритма

SOLLIN.

**&.5.6. Алгоритм SOLLIN (доказательство). Восстановите опущенные детали доказательства для алгоритма SOLLIN.

5.5.7. Алгоритм PARSORT (анализ). Какие исходные конфигурации заставляют алгоритм PARSORT выполнить наибольшее количество обменов?

**5.5.8. Алгоритм PARSORT (анализ). Предположим, что все размещения равновероятны. Каково среднее число обменов местами, производимых алгоритмом PAR-

***5.5.9. Кратчайшие пути (полное построение). Постройте полностью алгоритм отыскания кратчайшего пути между двумя заданными произвольными вершинами в сеги, веса ребер в которой означают их длины. Последовательные алгоритмы отыскания кратчайших путей представлены в разд. 6.2.

Глава 6. Математические алгоритмы

На протяжении этой книги мы уже иллюстрировали многие концепции и методы, строя алгоритмические решения математических задач. В трех разделах этой главы содержится несколько дополнительных примеров.

В разд. 6.1 мы рассмотрим две игры и комбинаторную головоломку. Для всех трех задач будут построены самые эффективные стратегии и решения. Эти примеры представляют большое число игр и головоломок, решения которых просты и остроумны.

В разд. 6.2 ставится задача отьюкания кратчайшего пути между двумя заданными вершинами в сети. Эта задача имеет много важных приложений в исследовании операций и вычислительной математике. Как мы увидим, алгоритм, построенный в этой главе, оказывается фактически идентичным алгоритму PRIM (гл. 4).

В разд. 6.3 рассмотрены алгоритмы, использующие случайные числа. Первый из этих алгоритмов дает эффективный способ выбора случайного набора М объектов из множества N (MN) объектов. Остальная часть этого раздела посвящена алгоритмам генерации случайных чисел.

6.1. Игры и комбинаторные головоломки

В этом разделе мы изучим классическую комбинаторную головоломку и две игры, что позволит проиллюстрировать ряд интересных процедур.

В нескольких местах этой книги изучались другие игры, например головоломка «8» и тур коня в разд. 2.1 и 3.3 соответственно. В алгоритмах решения этих задач применялись поисковые и эвристические методы, использующие скорость и вычислительную мощность компьютера. Большинство машинно-ориентированных реализаций игр характеризуется тем же. В данном разделе будут приведены различные примеры. Каждый содержит очень эффективный точный алгоритм, который настолько прост, что его труднее реализовать в виде машинной программы, чем выполнить с помощью карандаша и бумаги.

Магические квадраты

Магическим квадратом порядка N называется такое расположение целых чисел в матрице NxN, что суммы элементов по каждой строке, каждому столбцу и двум главным диагоналям совпадают.