Двоичный поиск можно теперь интерпретировать как прохождение этого дерева от корня до искомой записи. Если достигнута конечная вершина, а заданный ключ не найден, искомая запись в данном файле отсутствует. Заметим, что число вершин на единственном

8 9 10 11 12 13 14 15

7 14 27 33 42 49 51 БЗ 67 70 77 в1

1 = 8

89 94 95 99

изт=1б1

7 14 27 33 42 49 51 tplRSTl t=4 tl

LAST=7

42 49 51

FIRSTst t tl AST=7 1 = 6

FIRST =LAST= 1 = 5, K=.Ks, ВОЗВРАТ

Рис. 5.2.2. Использование алгоритма BSEARCH для отыскания записи с ключом 42,

пути от корня к заданному ключу К равно числу сравнений, выполняемых алгоритмом BSEARCH при попытке отыскания /С.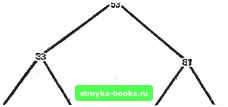

А Л Л Л

Рис. 5.2.3. Представление файла с рис. Б.2.2 в виде двоичного дерева, построенного с помощью алгоритма BSEARCH,

представление упорядоченного файла в виде двоичного дерева оказывается полезным при анализе алгоритма BSEARCH. Для удобства предположим, что число N записей в файле таково, что iV=2*-1 при некотором положительном целом k. В этом случае двоичное дерево является полным, т. е. у каждой внутренней вершины есть как левый, так и правый преемники, дерево имеет высоту k-l, а число вершин на уровне i равно 2, при f=0, 1, . . ., k-l.

Вначале рассмотрим наихудший случай работы алгоритма BSEARCH. Очевидно, что число сравнений является первоочередным фактором, определяющим его сложность. Число сравнений, необходимых для отьюкания заданного ключа, на единицу превосходит уровень ключа в дереве. В худшем случае мы должны пройти дерево до конечной вершины, т. е. произвести k=logs{N-{-l) сравнений. Таким образом, алгоритм BSEARCH в худшем случае имеет сложность O(logaiV).

Вычисление среднего числа сравнений для успешного поиска будет несколько сложнее. Предположим, что все записи встречаются равновероятно. Пусть NCOMP (i) будет уровнем ключа Кг в двоичном дереве, увеличенньм на единицу. Тогда NCOMP(f) равно числу сравнений, необходимых для отыскания Ki. Среднее число сравнений равно

C = JiVCOMP(0. 1=1

Так как мы считаем двоичное дерево полным и N=2>-1, существует

2*-* вершин уровня k-l. Если обозначить через а сумму 2NC0MP(t),

1 = 1

то а является суммой первых N членов ряда

a=l+2-f 2 + 3-f З + 3-f 3-Ь...

1 + 2 (2) + 23) + 2М4) + • . + (/) + ...+ 2*-1 (k).

Выражение для а в замкнутой форме можно получить, используя стандартный вычислительный прием. Если обозначить через 5, сумму k членов геометрической прогрессии, то

Пусть y=2z, тогда

Далее

S, (2г} l + 2z + i2zf + ... + (2)*-* igi. [{Sk(22)~l}z] = 2 {2z) + 2(3z) + ... + 2*-i (fe*-i).

почленно дифференцировали ряд {S,(2z)-1}г. Если вычислить

эту производную при 2=1 и прибавить 1, то мы получим а, т. е. G == 1 +-[{S,i(2z) - 1}z] при z == 1 (проверьте это).

Используя выражение для частичной суммы геометрической прогрессии в замкнутой форме, получим

0 = 1 + 2-1);

- а i+2*(fe l) l+(jV+l)[log,(Af+l) l] N+l, ,r, , ~1Г--N ~ N N

Таким образом, средняя сложность двоичного поиска равна 0{logz). Сопоставьте э1гот результат со средним числом сравнений NJ2 для алгоритма последовательного поиска (см. упр. 5.2.4).

До сих пор мы обсуждали только файлы с фиксированным числом записей. Теперь рассмотрим случай переменного размера файла, т. е. файла, в котором записи можно вставлять и удалять.

Сначала разработаем алгоритм обслуживания растущего файла записей, упорядоченных по ключам. Для этого йужно выбрать удобную структуру данных и соответствующий алгоритм, который быстро найдет данную запись в структуре, если она там содержится, или вставит запись на подходящее место, если ее там нет.

Какие структуры данных мы будем использовать? Связанные списки - одна из возможных структур. В разд. 2.3 мы видели, что этот тип структуры данных позволяет эффективно производить вставление и удаление элементов. К сожалению, нелегко выполнять двоичный поиск в связанных списках.

Существует ли другая структура данных, которая позволяла бы сохранить эффективность двоичного поиска и в то же время позволяла бы эффективно вставлять или удалять записи? Далее мы покажем, что двоичное дерево является хорошим решением этой проблемы-

В приведенной ниже таблице указаны 10 городов, упорядоченных по убыванию численности населения (йа 1970 г.). Числа в правом столбце показывают алфавитный порядок. Прочтем эти города в алфавитном порядке и запомним их в двоичном дереве в порядке возрастания численности населения.

Энн Арбор первый на входе, и он становится корнем дерева. Шар-лоттсвилль следующий, он сравнивается с корневой вершиной. Так как население Шарлоттсвилля меньше населения Энн Арбора, то Шарлоттсвилль становится левым преемником Энн Арбора. Каждый из последующих городов читается и сравнивается с корнем. Если его население меньше, чем у корня, он далее сравнивается с левым преемником корня; если больше, то с правым. Раньше или позже каждый город сравнивается с вершиной, не имеющей правого или левого преемника, и он становится новой конечной вершиной этого дерева. Пронумерованные фиктивные вершины будут использованы для обозначения недостающих преемников для городов, не имеющих