Подстановка этого неравенства в (2) дает

Q (N) cN + + KN In N

Наконец, поскольку Ж>2, имеем

4& КЛ !(2с+2&) W

гЛ/4- -<Г -

Таким образом.

2 N-l N

Рис. 5.1.3. Вогнутая функция.

Поэтому средней оценкой трудоемкости алгоритма QUICKSORT является 0{N In N). Последнее замечание об этом алгоритме касается значения М, обусловливающего сортировку коротких подпоследовательностей; более детальный анализ сложности QUICKSORT - см. [59] - показывает, что подходящим значением является М==9.

HEAPSORT: Алгоритм сортировки,

имеющий в худшем случае порядок 0(N log N)

Существует не много алгоритмов сортировки, которые в худшем случае могут гарантировать не более О {N log N) сравнений. Одним из них является предложенный Вильямсом остроумный алгоритм, использующий специальную структуру дерева, называемую пирамидой. Пирамида состоит из помеченного корневого двоичного дерева заданной высоты h, обладающего следующими тремя свойствами:

1. Каждая конечная вершина имеет высоту h или h-1.

2. Каждая конечная вершина высоты h находится слева от любой конечной вершины высоты h-1.

3. Метка любой вершины больше метки любой следующей за ней вершины.

Из свойства 3 непосредственно вытекает, что метка корня пирамиды является наибольшей меткой дерева. На рис. 5.1.4 изображены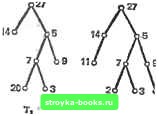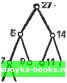

57 Srf 5Ь 411 Ь7

Ыо г6 Ъз 2/ Ьз

Т« Тз т..

Рис. 5.1.4. Только дерево является пирамидой.

три помеченных корневых двоичных дерева, не являющихся пирамидами, и одно (Т) - пирамида. Заметим, что для дерева Tt не выполняется свойство i при i=l, 2, 3.

Специальная структура пирамид позволяет компактно размещать их в памяти. В частности, мы можем разместить пирамиду с п вершинами в массиве А, в котором две непосредственно следующие за вершиной из A(i) вершины помещаются в A{2i) и Л (2+1). Например, пирамиду Гд, изображенную на рис. 5.1,4, можно разместить в массиве А из девяти элементов следующим образом:

12 345 6789

А 27 9 14 8 5 11 7 2 3

Заметим, например, что элементы 11 и 7 в Л(6) и А(7) - это те два элемента, которые следуют за элементом 14 в Л (3). Если 2t>n, тогда за вершиной Л (i) не следуют другие вершины, и она является конечной вершиной пирамиды. Этот порядок расположения элементов пирамиды такой же, как и порядок при методе поиска в ширину по дереву (см. разд. 3.5).

Используя такое представление массива, легко отсортировать вершины пирамиды. Проиллюстрируем это на пирамиде Т.

1. Переставляем Л(1) с А(п). Таким образом.

27 9 14 8 5 И 7 2 3

преобразуется в

3 9 14 8 5 11 7 2 27

что эквивалентно замене деревом на рис. 5.1.5.

2. Устанавливаем n<-n-1. Это эквивалентно вычеркиванию вершины 27 из на рис. 5.1.5.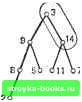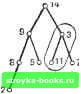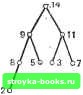

3 9 14 8 5 11 7 2 27

3 9 14 2 5 11 7 2 14 9 3 8 5 11 72 14 Э 11 8 5 3 7 2

27 Та

3-27пгрЕ1!гавлевы тервстгнша 3-14 лерестановка 3-11

Рис. 5.1.5. Первые шаги при сортировке вершин пирамиды Т, представленной на

рис. 5.1.4.

3, Преобразуем модифицированное дерево в другую пирамиду. Это достигается повторением перестановки нового корня с большей из двух новых непосредственно следующих за ним вершин до тех пор, пока он не станет больше, чем обе вершины, непосредственно за ним следующие. В Т, переставлены вершины 3 и 14, а в Tg в соответствии с этой процедурой переставлены вершины 3 и 11. Поэтому - преобразованная пирамида.

4. Повторяем шаги 1, 2 и 3 до тех пор, пока не получим п=1. Рис. 5.1.6 иллюстрирует завершение этого процесса сортировки

для пирамиды на рис. 5.1.5.

Поскольку для такой процедуры сортировки на входе требуется пирамида, нам нужен алгоритм для преобразования произвольного массива целых чисел в пирамиду. Такой алгоритм использует шаг 3 ранее описанного процесса. Это иллюстрируется на массиве цеЛых чисел - рис. 5.1.7,0;. Начнем с предположения, что целые числа этого массива расположены в корневом двоичном дереве, как было бы в случае, если в массиве была бы размещена пирамида - рис. 5.1.7, б. затем проходим справа налево весь массив, проверяя, больше ли А (i), чем А (21) и Л(21Ч-1) для i=ln/2 \, . . ., 1 (рис. 5.1.8). Если для какого-то значения i А (i) не больше, чем А (2i) и А (2t+l), то npHSie-