2X3 1 8 4 7 6 6

х2 3 1 8 4 7 6 5

{/роееньЪ

Урсйёт Б

X 2 3 1 7 4 6 8В

1 2 3 6 7 4 X 8 в

X 1 3 7 2 4

6 В В

1 3 X 7 2 4 6 8 Б

1 2 X 7 4 3 6 8 5

1 2 3 7 4 5 6 8 X

1 2 3 7 Х- 8 6 5 4

1 2 X 7 8 3 6 5 4

Уровень 7

Рис. 3.3.4. Дерево отходов, построенное для получения конфигурации в вершине 20.

L3.3.2. Пример с головоломкой «8» (реализация). Дайте полное формальное описание алгоритма с отходами для головоломки «8». Напишите программу и примените ее в упр. 3.3.1.

*3.3.3. Задача восьми ферзей (разработка). Покажите, что максимум восемь ферзей могут быть расположены на стандартной шахматной доске 8x8 таким образом, что ни один ферзь не бьет другого. Разработайте алгоритм с отходами, в явном виде создающий такую конфигурацию.

.L3.3.4. Задача восьмиферзей (реализация). Реализуйте алгоритм в упр. 3.3.3.

**3.3.5. Алгоритмы с отходами (общая формулировка). Попытайтесь дать детальную, общую, теоретико-множественную формулировку основной структуры, характерной для всех алгоритмов с отходами.

***3.3.6. Алгоритмы с отходами (ашлиз). Обычно почти невозможно провести очень точный анализ ожидаемой трудоемкости алгоритма с отходами. Как можно грубо оценить среднее время работы алгоритмов с отходами? Охарактеризуйте сильные и слабые стороны этих способов оценки. Опробуйте их на реальной программе с отходами (см. упр. 3.3.2 и 3.3.4).

3.4. Метод ветвей и границ

Метод, известный как метод ветвей и границ, похож на методы с отходами назад тем, что он исследует древовидную модель пространства решений и применим для широкого круга дискретных комбинаторных задач. Алгоритмы с отходами нацелены на то, чтобы найти одну или все конфигурации, моделируемые Л-векторами, которые удовлетворяют определенным свойствам. Алгоритмы ветвей и границ ориентированы в большей степени на оптимизацию. В решаемой задаче определена числовая функция стоимости для каждой из вершин, появляющихся в дереве поиска. Цель - найти конфигурацию, на которой функция стоимости достигает максимального или минимального значения.

Алгоритм ветвей и границ хорошо работает в задаче коммивояжера, рассмотренной в разд. 1.3. В данном разделе изложение будет вестись на примере задачи коммивояжера. Предупреждаем читателя, что алгоритмы ветвей и границ, как правило, бывают довольно сложны и представленный здесь - не исключение. При помощи алгоритмов ветвей и границ удалось решить большой круг разнообразных серьезных практических задач (см. гл. 7); эти алгоритмы редко оказываются простьми.

Напомним, что задача заключается в нахождении в торговом участке коммивояжера тура из N городов с наименьшей стоимостью. Каждый город входит в тур только один раз. В терминах сетей в сети городов надо найти покрывающий цикл наименьшей стоимости. Имеется матрица С, каждый элемент которой cij равен стоимости (обычно в единицах времени, денег или расстояния) прямого проезда из города i в город /. Задача называется симметричной, если си=сц для всех i и /, т. е. если стоимость проезда между каждыми двумя городами не зависит от направления. Предположим, что Сц=оо для всех i.

Алгоритмы ветвей и границ для задачи коммивояжера могут быть сформулированы разными способами. Авторы излагаемого алгоритма - Литл, Мерти, Суини и Карел. Это своего рода классика.

Во-первых, рассмотрим ветвление. На рис. 3.4.1, а показана матрица стоимостей для асимметричной (несимметричной) задачи коммивояжера с пятью городами, представленной на рис. 3.4.1, б. Обратите внимание на то, что мы пользуемся направленной сетью, чтобы указать стоимости, так как стоимость проезда из города i прямо в город / не обязательно такая же, как стоимость проезда из города / в город L Корень нашего поискового дерева будет соответствовать множеству «всех возможных туров», т. е. эта вершина представляет множество всех 4! возможных туров в нашей задаче с пятью городами. В общем случае для любой асимметричной задачи с N городами корень будет представлять полное множество R всех (/V-1)! возможных туров. Ветви, выходящие из корня, определяются выбором одного ребра, скажем (i, J). Наша цель состоит в том, чтобы разделить множество

всех туров на два множества: одно, которое, весьма вероятно, содержит оптимальный тур, и другое, которое, вероятно, не содержит. Для этого выбираем ребро (i, j); оно, как мы надеемся, входит в оптимальный тур, и разделяем R на два множества {t, /} и {i, /}. В мно-жество {i, j) входят туры из R, содержащие ребро (t, /), а в (t, /} - не содержащие (J, /).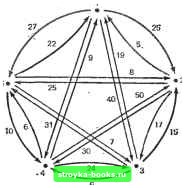

Рис. 3.4.1. Задача коммивояжера: (а) матрица стоимостей; (б) сеть из пяти городов.

Предположим, в нашем примере мы производим ветвление на ребре (j, /)= (3,5), имеющем наименьшую стоимость во всей матрице. Корень и первый уровень дерева пространства решений будут тогда такими, как показано на рис. 3.4.2. Заметим, что каждый тур из R

/6 О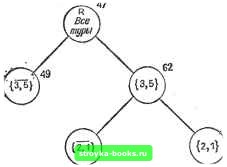

!/ро£ень г

Рис. 3.4.2. Построение дерева поиска по методу ветвей и границ.

содержится только в одном множестве уровня 1. Если бы мы как-то могли сделать вывод, что множество {3, 5} не содержит оптимального тура, то нам нужно было бы исследовать только множество {3, 5}.