Схема, которую мы только что изобразили,- это частный случаи известного в математике графа, или сети. В общем случае сеть - это множество точек (на плоскости) вместе с линиями, соединяющими некоторые или все пары точек; над линиями могут быть проставлены веса.

Для простоты предположим, что у Джека только пять городов, для которых матрица стоимостей показана на рис. 1.3.1, а. Тогда сетевая модель может быть изображена, как иа рис. 1.3.1, б. Предположим также, что стоимость проезда из города i в город / такая же, как и из / в i, хотя это и необязательно.

Гврод

3 4В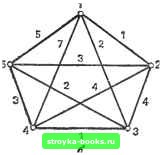

Рис. 1.3.1. Задача коммивояжера с пятью городами.

Что МЫ ищем В задаче? В терминах теории сетей список городов (который мы ранее описали) определяет замкнутый цикл, начинающийся с базового города и возвращающийся туда же после прохождения каждого города по одному разу. Такой цикл соответствует неотрывному движению карандаша вдоль линий сети, которое проходит через каждую точку только один раз и начинается и оканчивается в одной и той же точке. Обход такого рода назовем туром. Стоимость тура определяется как сумма весов всех пройденных ребер. Задача решена, если мы можем найти тур с наименьшей стоимостью.

На рис. 1.3.1,6 обход 1-5-3-4-2-1 есть тур со стоимостью 5-1-2+1+4+1 = 13. Является ли он туром с минимальной стоимостью?

Рассмотренная задача известна в литературе как задача коммивояжера; она стала в какой-то мере классической. Это один из наиболее известных примеров таких задач, которые очень легко поставить и промоделировать, но очень трудно решить. Время от времени мы будем возвращаться к этой задаче в целях иллюстрации.

Разработка алгоритма

Как только задача четко поставлена и для нее построена модель, мы должны приступить к разработке алгоритма ее решения. Выбор метода разработки, зачастую сильно зависящий от выбора модели,

может в значительной степени повлиять на эффективность алгоритма решения. Два разных алгоритма могут быть правильными, но очень сильно отличаться по эффективности. В одном из следующих разделов этой главы обсуждаются критерии эффективности.

Пример. Вернемся к коммивояжеру из предыдущего раздела. Постановка задачи и модель, описанные ранее, наводят на мысль о следующем алгоритме.

Сначала произвольно перенумеруем п городов целыми числами от 1 до п, присваивая каждому городу свой номер. Базовому городу приписываем номер п. Заметим, что каждый тур однозначно соответствует перестановке целых чисел 1,2,..., п-1. Действительно, каждый тур соответствует единственной перестановке, и каждая перестановка соответствует единственному туру. Такое соответствие называется взаимно-однозначным. Таким образом, для любой данной перестановки мы можем легко проследить соответствующий тур на сетевой модели и в то же время вычислить стоимость этого тура.

Можно решить задачу, образуя все перестановки первых п-1 целых положительных чисел. Для каждой перестановки строим соответствующий тур и вычисляем его стоимость. Обрабатывая таким образом все перестановки, запоминаем тур, который к текущему моменту имеет наименьшую стоимость. Если мы находим тур с более низкой стоимостью, то производим дальнейшие сравнения с этим туром.

Algorithm ETS (Исчерпывающий коммивояжер). Решить задачу коммивояжера с городами, последовательно рассматривая все перестановки из -1 положительных целых чисел. Таким образом мы рассмотрим каждый возможный тур и выберем вариант TOUR с наименьшей стоимостью MIN, Алгоритм ETS требует в качестве входных данных число городов N и матрицу стоимостей С.

Шаг 0. [Инициализация, т. е. установка в начальное состояние]

Set TOUR0; and MINoo. Шаг 1. [Образование всех перестановок] For /-<-1 to (N-1)! do

through шаг 4 od; and STOP.

Шаг 2. [Получение новой перестановки] Set Р--Т-я перестановка целых чисел 1,2,..., N-1. (Заметим, что здесь нужен подалгоритм.)

Шаг 3. [Построение нового тура] Строим тур Т{Р), соответствующий перестановке Р; and вычисляем стоимость COST {Т(Р)). (Заметим, что здесь нужны два других подалгоритма.)

Шаг 4. [Сравнение] И COST (Г(Р))<М1Ы then set TOUR Т{Р); and MINCOST {Т{Р)) fi.

Алгоритм ETS - неплохое первое приближение к точноглу алгоритму. Ему недостает некоторых важных подалгоритмов, и он недо-

статочно близок к окончательной программе. Эти недостатки будут устранены позже.

Похоже, что существует тенденция: программисты затрачивают относительно небольшое время на стадию разработки алгоритма при создании программы. Проявляется сильное желание как можно быстрее начать писать самое программу. Этому побуждению не надо поддаваться. На стадии разработки требуется тщательное обдумывание, следует также уделить внимание двум предшествующим и первым трем следующим за стадией разработки этапам. Как и следует ожидать, все восемь основных этапов, перечисленных в разд. 1Л, нельзя рассматривать независимо друг от друга. В особенности первые три сильно влияют на последующие, а шестой и седьмой этапы обеспечивают ценную обратную связь, которая может заставить нас пересмотреть некоторые из предшествующих этапов.

Правильность алгоритма

Доказательство правильности алгоритма - это один из наиболее трудных, а иногда и особенно утомительных этапов создания алгоритма.

Вероятно, наиболее распространенная процедура доказательства правильности программы - это прогон ее на разных тестах. Если выданные программой ответы могут быть подтверждены известными или вычисленными вручную данными, возникает искушение сделать вывод, что программа «работает». Однако этот метод редко исключает все сомнения; может существовать случай, в котором программа не сработает.

Мы предложим следующую общую методику доказательства правильности алгоритма. Предположим, что алгоритм описан в виде последовательности шагов, скажем, от шага О до шага rri. Постараемся предложить некое обоснование правомерности для каждого шага. В частности, может потребоваться лемма об условиях, действующих до и после пройденного шага. Затем постараемся предложить доказательство конечности алгоритма, при этом будут проверены все подходящие входные данные и получены все подходящие выходные данные.

Пример. Алгоритм ETS настолько прост, что его правильность легко доказать. Поскольку проверяется каждый тур, должен быть проверен и тур с минимальной стоимостью; как только до него дойдет очередь, он будет запомнен. Он не будет отброшен - это может случиться только в том случае, если существует тур с меньшей стоимостью. Алгоритм должен закончить работу, так как число туров, которые нужно проверить, конечно. Подобный метод доказательства известен как «доказательство исчерпыванием»; это самый грубый из всех методов доказательства.

Подчеркнем тот факт, что правильность алгоритма еще ничего не говорит о его эффективности. Исчерпывающие алгоритмы редко бывают хорошими во всех отношениях.