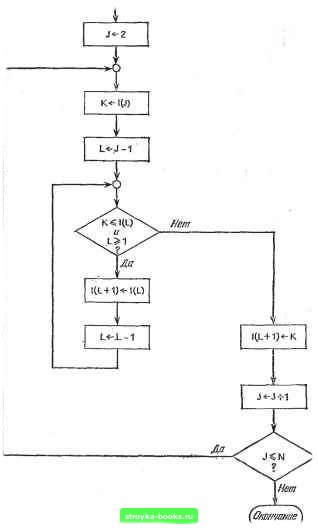Рис. 2.4.1. Блок-схема алгоритма SIS.

t+1 ВОЗМОЖНЫХ позиций для следующего ключа. Предположим, что новый ключ с равной вероятностью может быть помещен в лю-

бой из этих промежутков. Пусть Xi - случайная переменная, равная, числу сравнений, требуемых для помещения ключа i+1 в правильную

позицию на этом проходе. Тогда

ЕШ- ()+2()+з() + ...+- + = =-U+2 + 3+...+{i-l) + i + i] =

..... 1 t (t+1)

i+1 i

(используем формулу Гаусса)=

Заметим, что, когда нужная позиция находится на дальнем конце, выполняется только i сравнений. Так как имеется N ключей, в цикле на шаге 1 выпояется N-1 итераций. Если случайная переменная Y обозначает общей число сравнений при сортировке, то

Используя результат из упр. 2.4.11, получим EIY]=E [X,]+£ [XJ +...+£ =

= а+1) + (1+1) + -+(

Л-1 , n - 1

= [1 + 2+...+(Л-1)] +

N-1 N-1

1 + 1 +

n - 1

£-1

т 3N г - -4--

N J

где Hrf=y\ называется N-m гармоническим числом). i=i

Таким образом, среднее число сравнений, требуемых алгоритмом SIS для сортировки N ключей, приблизительно равно N/A, а средняя сложность равна 0{N). С помощью аналогичного анализа можно обнаружить, что среднее число перемацений I{L+l)<-I{L) также

Алгоритм SIS не является очень хорошим алгоритмом сортировки, хотя, впрочем, он один из простейших и наиболее удобных для реализаций. В разд. 5.1 будут изучены более сложные алгоритмы сортировки со средней сложностью и сложностью в худшем случае 0{N log N).

На примере сортировки методом прямого включения мы продемонстрировали простой вероятностный анализ сложности. Далее в книге мы будем часто прибегать к подобному анализу.

) Когда N- оо, Яг приблизительно равно In n+0,577+0(1/N).

Чтобы показать основное различие между вероятностным и статистическим подходом, вернемся к нашему анализу ожидаемой трудоемкости алгоритма SIS. По заданному или предполагаемому распределению сортируемых элементов мы вычислили ожидаемое число сравнений, выполняемых при сортировке ключей. При этом мы воспользовались определениями и правилами вычисления из теории вероятностей. Таким образом, заданное распределение было использовано для предсказания поведения алгоритма. Этот тип анализа характерен для большинства вероятностных моделей.

Во многих отношениях статистические задачи «обратны» вероятностным задачам. Наблюдается поведение системы и делается попытка вывести заключения о лежащем в основе неизвестном распределении случайных величин, которые описывают функционирование системы. Определим случайную переменную Y, которая равна для любой слу чайной последовательности N целых чисел числу сравнений, требуемых алгоритмом SIS для сортировки этой последовательности. Каждое применение алгоритма SIS к случайной последовательности целых чисел дает, таким образом, выборку У. Хотя нам и не известно распределение Y, мы можем взять несколько выборок, вычислить среднее Y от этих полученных экспериментальным путем чисел и принять Y как оценку математического ожидания Y (т. е. использовать F для аппроксимации Е [Y]). Следовательно, для вывода заключений о случайной переменной используются полученные из наблюдений значения.

Не представляется возможным дать общие рекомендации относительно того, какая из форм анализа лучше. На практике они должны дополнять друг друга. В нашем примере мы сделали предположение о распределении и затем смогли вычислить Е [Y] вероятностными методами. То есть мы предположили, что (1+1)-й ключ с равной вероятностью может оказаться помещенным в любую из позиций на концах или внутри отсортированного списка из i элементов. Верно ли это предположение для «реальных» данных? С другой стороны, статистическая оценка для Е IY] может оказаться плохой из-за того, что наблюдаемая выборка была в некотором смысле «непредставительной». Если нам сдали случайным образом четыре карты и все они оказались тузами, будем ли мы считать, что вся колода состоит только из тузов? Если провести оба анализа - сравнить статистическую оценку Y с выведенным значением Е [Y] - и значения окажутся близкими, будут основания считать, что мы кое-что знаем о средней трудоемкости алгоритма. Если они сильно отличаются, возникает причина для беспокойства.

Продолжим обсуждение оценок и статистического анализа алгоритмов в несколько более общих терминах. Нас интересует ожидаемая или средняя трудоемкость некоторого алгоритма А на множестве возможных исходных данных D. Множество D очень велико, и алгоритм А достаточно сложен. Рассмотрим обработку алгоритмом А некоторых случайным образом выбранных из D исходных данных как экспери-