
 |
|
Главная Полное построение алгоритма [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [ 16 ] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] в) (г) Л1 < x 2; [log,(M+l)-l]<L< Доказательство теоремы оставлено в качестве упражнения. Остовное дерево для сети G есть остовная подсеть, являющаяся деревом. На рис. 2.2.15 приведены взвешенная сеть G и некоторые из ее остовных деревьев с их весами. Сколько у сети остовных деревьев? Легко показать следующее. Теорема 2.2.6. Сеть G связна тогда и только тогда, когда она содержит остовное дерево. Изоморфизм Этот раздел мы завершим кратким рассмотрением следующей важной задачи. Если у нас есть два представления сети, то, как узнать, не описывают ли они одну и ту же сеть? Очевидно, сначала нужно определить, что подразумевается, когда мы говорим, что «две сети одинаковы». Две сети G и G изоморфны, если существует взаимно-однозначное соответствие между вершинами G и G, такое, что две вершины и я v смежны в G тогда и только тогда, когда в G смежны соответствующие им вершины. Точнее, G=(]/, Е) изоморфна G= (]/, £") - это записывается в виде GG,- если существует взаимно-однозначная функция h из У в V, обладающая тем свойством, что {и, v)E тогда и только тогда, когда {h{u), h(v))E. Проблема определения, являются ли две сети изоморфными, неожиданно оказывается трудной. Для произвольных сетей все известные алгоритмы, гарантирующие правильный ответ, экспоненциальные. Фактически даже для небольших сетей эту задачу решить нелегко. Все три сети на рис. 2.2.16 изоморфны друг другу. Если вам это кажется очевидным, попытайтесь определить, какие сети изоморфны друг другу (если такие есть) из приведенных на рис. 2.2.17. Итак, проблема изоморфности очень трудна, как можно к ней подступиться? Хотя может и не оказаться возможным разработать алгоритм изоморфизма, являющийся полиномиальным в худшем случае, попытаемся сделать нечто полезное. 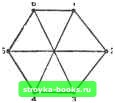 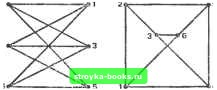 Рис. 2.2.16. Три изоморфные сети. Начнем с совершенно очевидного замечания. Из определения следует, что если сети G и С изоморфны и изоморфизм h найден, то любая вершина v степени d в G должна отображаться на вершину v=h{v) в G той же самой степени. 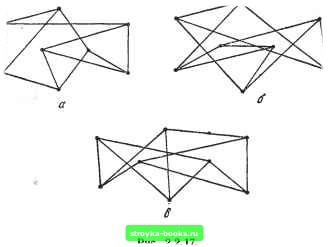 Что если мы попытаемся построить на этом наблюдении процедуру исчерпывающих проб и ошибок? Рассмотрим, например, две сети G и G: у каждой 10 вершин и каждая вершина степени 3. Любая из возможных взаимно-однозначных функций h т V в V будет удовлетворять указанному выше ограничению на степень; имеется 10! таких функций. Поэтому для решения вопроса об изоморфности G и G нам нужно было бы испытать каждую из 10! возможных функций, чтобы найти одну, удовлетворяющую требованию изоморфизма. Перед лицом этого комбинаторного взрыва исследователи часто отказываются от поиска эффективного алгоритма изоморфизма и взамен этого строят простые процедуры, от которых ожидается хорошая работа в большинстве случаев. Предпочитают также алгоритмы изоморфизма, пригодные для специальных классов сетей, появляющихся в некоторых приложениях. Инвариантом сети G называется параметр, имеющий одно и то же значение для всех сетей, изоморфных G. Среди самых очевидных инвариантов отметим следующие: 1. Число вершин. 2. Число ребер. 3. Число компонент. 4. Последовательность степеней, т. е. список степеней всех вершин в убывающем порядке значений. в контексте данной книги эвристический алгоритм обладает следующими двумя свойствами: 1. Он находит, как правило, хорошие, хотя и не обязательно оптимальные, решения. 2. Его легче и быстрее реализовать, чем любой из известных точных алгоритмов (т. е. алгоритмов, гарантирующих оптимальное решение). Более полное рассмотрение таких алгоритмов можно найти в разд. 3.2. Эвристики для решения задач изоморфизма обычно состоят в попытках показать, что две рассматриваемые сети не изоморфны. Для этого составляется список различных инвариантов в порядке, определяемом сложностью вычисления инварианта. Затем последовательно сравниваются значения параметров сетей. Как только обнаруживаются два различных значения одного и того же параметра, приходят к заключению, что данные сети неизоморфны. К сожалению, не известно множества инвариантов, которое позволило бы этой процедуре установить за полиномиальное время, что сети изоморфны. Такое множество (неизвестно, будет ли оно когда-нибудь найдено) называется кодом сети. По существу, эвристический алгоритм рассматриваемого типа сводится к сравнению неполных кодов двух сетей. Конечно, рассмотрение большего числа инвариантов увеличивает вероятность правильного заключения об изоморфизме при совпадении всех значений параметров, но в общем случае ничего не гарантирует. Например, для двух пятивершинных сетей на рис. 2.2.18 все четыре из перечисленных выше инвариантов совпадают, но эти сети не изоморфны. Рассмотрим теперь пример достаточно сложной эвристики, работающей с матрицей смежности А (G). Сама по себе матрица смежности не является инвариантом, хотя если G и d изоморфны, то при некотором переупорядочивании столбцов и строк Л(G) мы получаем A{G,). Если у сетей G и Gi М вершин, то поиск нужной последовательности перестановок строк и столбцов требует в худшем случае 0(М\) операций. Впрочем, описьшаемая ниже полиномиальная процедура справ-  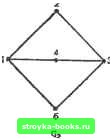 Рис. 2.2.18. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [ 16 ] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] 0.0013 |