
 |
|
Главная Полное построение алгоритма [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [ 15 ] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] дом из этих двух деревьев на 1 меньше числа вершин. Отсюда следует утверждение (б). Из утверждения (б) следует утверждение (в). Если.сеть Т несвязна, Х- X Рис. 2.2.12. Все различные деревья с шестью вершинами. то каждая компонента Т связна и не имеет циклов. Поэтому из утверждения (б) число вершин в каждой компоненте превышает число ребер на 1. Далее следует, что общее число вершин в Г по крайней мере на 2 больше, чем общее число ребер, что противоречит предположению (б). 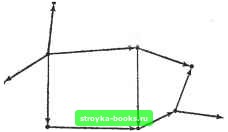 Рис. 2.2.13. Ациклическая ориентированная сеть. Из утверждения (в) следует утверждение (г). Сначала докажем следующую лемму. Лемма. Если в сети G имеется М вершин, N ребер и К компонент, то M-K<:N. Доказательство. Проведем индукцию по числу ребер. Для N=1 утверждение леммы очевидно. Пусть G содержит наименьшее возможное количество ребер, скажем No. Удаление любого ребра из G должно поэтому увеличивать К на единицу, оставляя в сети М вершин, /<"+! компоненту и No-l ребро. Из предположения индукции следует, что No-lM-(/C+l), т. е. NM-К- Это доказывает лемму, так как N>No. Из утверждения (в) и доказанной леммы путем сведения к противоречию получаем утверждение (г), так как K=i и удаление любого ребра оставляет УИ - 2 ребра и М вершин. Из утверждения (г) следует утверждение (д). Каждая пара вершин соединяется по крайней мере одним путем, так как сеть Т связна. Если каждая пара вершин соединяется двумя или более различными путями, то любые два таких пути образуют цикл; отсюда следует противоречие, так как никакое ребро в таком цикле не может быть мостом по теореме 2.2.3. Из утверждения (д) следует утверждение (е). Если Т содержит цикл, то любые две вершины в этом цикле должны быть связаны по крайней мере двумя путями. Если к Т добавляется ребро /, то в T+I между тупиковыми вершинами / будут существовать два пути [ребро / и единственный путь, задаваемый утверждением (д)]. Это единственный цикл в T+I, потому что любой другой цикл также должен был бы содержать ребро /. Отсюда следовало бы существование двух вершин в Г, между которыми имеется по крайней мере два различных пути,- противоречие с утверждением (д). Из утверждения (е) следует утверждение (а). Предположим, что сеть Т несвязна. Если мы добавим к Т ребро, которое соединяет вершины в двух компонентах, то цикла создать нельзя; это противоречит утверждению (е). Поэтому Т должна быть связна, и теорема.2.2.4 доказана. Следствие 2.2.4. Каждое дерево с УИ2 вершинами имеет по крайней мере две тупиковые вершины. Доказательство непосредственно следует из теорем 2.2.1 и 2.2.4. Дерево, у которого одна вершина выделяется среди всех других, называется корневым деревом; выделенная вершина называется корнем дерева. Как правило, корневые деревья изображаются так, что корень оказывается наверху, а все остальные вершины - ниже его, на уровнях, соответствующих расстоянию от корня. Иллюстрация приведена на рис. 2.2.14, а. Мы будем предполагать, что каждое дерево с корнем имеет по крайней мере три вершины. Максимальный уровень любой вершины в дереве с корнем известен как высота дерева. Среди наиболее широко используемых математических структур употребляется один специальный класс корневых деревьев, известных как двоичные корневые деревья. С ними нам часто придется встречаться в этой книге. Двоичное корневое дерево - это корневое дерево, у которого степень корня равна 2, а степень всех остальных вершин 1 или 3. Одно такое дерево приведено на рис. 2.2.14, б. Теорема 2.2.5. Пусть Т - двоичное корневое дерево, у которого М вершин, вьюопш L и Q тупиковых вершин. Тогда (а) М нечетно; (б) Q = ; Корень 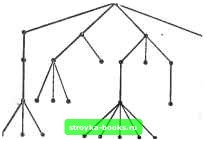 Уровень О Корень 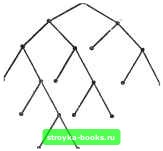 Уровень О Рис. 2.2.14. (а) Корневое дереве высоты 4; (б) двоичное корневое дерево высоты 5.  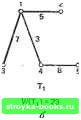 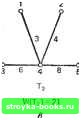 6485 м(Тз)-2е г 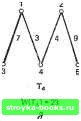 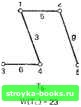 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [ 15 ] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] 0.0011 |