Рис. 2.2.9. Представление в форме векторов смежности.

МЫ ПРЕДПОЛАГАЕМ, ЧТО ЭЛЕМЕНТАМ МАССИВОВ NETW(I, J) И DEGREE (I) ПРИСВОЕНЫ

НАЧАЛЬНЫЕ ЗНАЧЕНИЯ О

ПРОЧЕСТЬ ЧИСЛО ВЕРШИН М И ЧИСЛО РЕБЕР N

READ( )М, N

ПРОЧЕСТЬ РЕБРА (U, V) ИЗ G

DO 1 К=1, N

READ ( ) и, V DEGREE (U) =DEGREE (U)--I NETW (U, DEGREE (U)) = V DEGREE (V) = DEGREE (V)+I NETW(V, DEGREE (V)) = и

CONTINUE

Еще одно полезное представление сети, с помощью списков смежности, обсуждается в разд. 2.3.

Воспользуемся некоторыми из рассмотренных нами сейчас понятий при разработке алгоритма определения связности сети и идентификации ее компонент, в случае когда сеть не связна. Такой алгоритм может оказаться очень полезной подпрограммой для более сложных процедур.

Главная идея алгоритма CONNECT (связывание) очень проста. Интуитивно хотелось бы свести компоненту к одной вершине. Это может быть сделано в процессе последовательного сведения, когда все смежные с данной вершины «сливаются» с ней. Вершина v сливаежя

с соседней вершиной и при удалении ребра (v, и), и отождествлении V с и. Одна результирующая вершина, обозначаемая через и, является смежной для каждой вершины, которая была см1жной для и и/или v перед слиянием. Эта операция проиллюстрирована на рис. 2.2.10.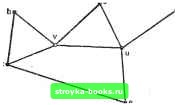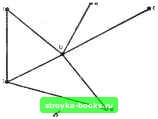

Рис. 2.2.10. процесс сведения (а) перед и (б) после слияния v с и.

Процедура будет состоять из выбора начальной вершины Vo и слияния с ней соседней вершины. Эта операция повторяется до тех пор, пока у Vo не останется смежных вершин. К этому моменту сведенная таким образом сеть будет состоять либо из одной вершины Vo, и в этом случае первоначальная сеть G была связной, либо у нас будет выделена одна из компонент G. Во втором случае выбирается новая начальная вершина и процедура повторяется. Таким образом можно выделить все компоненты.

Algorithm CONNECT (СВЯЗЫВАНИЕ) для определения связных компонент произвольной сети G. Переменная С - счетчик числа компонент.

Шаг 0. [Инициализация] Set Я G; and С 0. Шаг 1. [Получение очередной компоненты] While Н=0 do through шаг 5 od; and STOP. Шаг 2. [Выбор в Я вершины Fo]

Set Fo произвольная вершина из Я. Шаг 3. [Слить вершины с Vo\ While смежна по крайней мере с одной вершиной U в Н 6о шаг 4 od. Шаг 4. [Слияние] Пусть U - смежная с Vo вершина в Я. Set Я результирующая сеть после слияния и с Vo. (В этом цикле следует вести учет всех вершин, слитых с Vo. Для простоты здесь эту операцию учета мы опускаем.)

Шаг 5. [Удаление Vo] Set НH-Vo, and CC-fl.

Блок-схема для алгорит.ма CONNECT приводится на рис. 2.2.П. Доказательство правильности, реализация и анализ этого алгоритма оставлены в качестве упражнения.

Деревья

Дерево - это неориентированная связная сеть без циклов. Любая сеть без циклов называется лесом, а ее связные компоненты - деревьями. На рис, 2.2.12 приводятся все различные деревья с шестью вершинами. Весь рисунок можно считать лесом, состоящ,им из 36 вершин и 6 компонент.

Ориентированная сеть является деревом тогда и только тогда, когда она дерево с дугами, рассматриваемыми как неориентированные ребра Ациклическая ориентированная сеть не обладает ориентиро-Бан1ыми циклами. Ориентированная сеть на рис. 2.2.13 ациклична, но не является деревом. Следующая ниже теорема дает несколько других описаний деревьев.

Теорема 2.2.4. Пусть Т - сеть с вершинами. Тогда все сле-

дующие утмерждгния эквивалентны (т. е. если верно одно, то верны и все остальные):

(а) Т - дерево. Иначе говоря, Т связно и не имеет циклов.

(б) В сети имеется М-1 ребро и нет циклов.

(в) В сети Т имеется М-1 ребро и Т связна.

(г) Сеть Т связна, и каждое ее ребро - это мост.

(д) Любые две вершины в Т соединяются единственным путем.

(е) В сети Т нет циклов, но добавление любого нового ребра создает

ровно один цикл.

Доказательстмо. Из утверждения (а) следует утверждение (б). Так как Т не содержит циклов, удаление любого ребра разбивает Т на два дерева. Это следует из того факта, что ребро есть мост тогда и только тогда, когда оно не содержится ни в одном цикле (тео-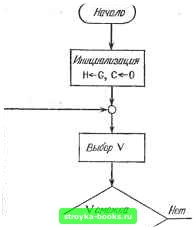

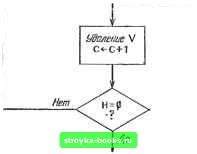Рис. 2.2.11. Блок-схема для алгоритма CONNECT (СВЯЗЫВАНИЕ).

рема 2.2.3). Индукцией по М. легко показать, что число ребер в каж-