Основные понятия

Сеть G=(V, Е) состоит из конечного множества V=V{G) М вершин (УИ1) и конечного множества E-E{G) Л/ неупорядоченных пар различных вершин (и, v) (Л/0), называемых ребрами G. Сеть Gi=(l/i, Ei) на рис. 2.2.3, а состоит из семи вершин Vi{t, и, v, w, х, у, г) и семи ребер £i={(a, v), (v, w), (w, x), {w, z), (z, v), (v, x), (w, y)}.

Очень важно понять, что сеть может быть изображена многими различными способами; например, сети, приведенные па рис. 2.2.3, б и в, те же, что и на рис. 2.2.3, а. Это следует из определения сети (убедитесь сами). В конце этого раздела задача, состоящая в том, чтобы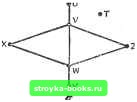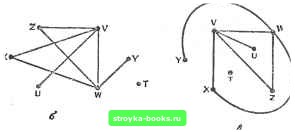

Рис. 2.2.3. Три способа изображения неориентированной сети.

определить, представляют ли два чертежа одну и ту же сеть, будет рассмотрена более подроб1ю.

Две вершины и hv являются смежными, если в G существует ребро (и, v); в противном случае и v, v независимы. Про ребро (и, v) также говорят, что оно инцидентно вершинам и и v.

Обратите внимание на то, что ребра состоят, как мы сказали, из неупорядоченных пар различных вершин. Таким образом, ребра не-ориентированы в том смысле, что ребра [и, v) и (v, и) считаются одним и тем же ребром. Более того, ребра вида [и, и), называемые петлями, не допускаются. Мы также не разрешаем наличия в сети мультиребер, т. е. двух или более копий данного ребра. Если в конкретных применениях рассматриваются и мультиребра, то сеть называется мультн-сетью (рис. 2.2.4).

Если мы изменим наше определение так, чтобы сеть состояла из конечного множества вершин и множества упорядоченных пар [и, v] различных вершин, то получим определение ориентированной сети; см. рис. 2.2.5, где У{Оа)={и, v, w, х, у, г) и E{G)={[u, v\, [v, w].

G,: V

Рис. 2.2.4. Мулыисеть с петлей в и.

Рис. 2.2.5. Ориентированная сеть.

[v, х], [х, да], [w, у], [w, z], [г, v]}. При работе с ориентированной сетью G={V, Е) элементы V обычно называют узлами, а элементы Е - дугами.

Если [и, v] - дуга ориентированной сети, то мы говорим, что и - левый сосед v, а v - правый сосед и.

Очень часто в практических применениях желательно приписывать ребрам или дугам сети веса для того, чтобы моделировать такие величины, как время, расстояние или стоимость. Взвешенная сеть - это такая сеть, ребрам или дугам которой поставлены в соответствие действительные числа.

Множество соседей вершины v N (v) это множество вершин, смежных с V, т. е. N{v)={u\ (и, v) Е}. Так, множество соседей вершины v на рис. 2.2.3, а состоит из вершин и, х, w и г. Степень вершины v, обозначаемая как d, или deg(u), равна числу вершин в N{v), т. е. dj,= deg(t))=A/(t))l. Таким образом, если вершины в d на рис. 2.2.3 расположить в порядке w, v, х, г, и, у, t, то их соответствующие степени есть 4,4,2,2,1,1,0, т.е. d=A, d„=4, <i=2 и т.д.

Вершина v называется тупиковой вершиной, если deg(u)=l; если deg(t))=0, то говорят, что v - изолированная вершина. На рис. 2.2.3, а вершины и Vi у тупиковые, а вершина t изолированная.

Теорема 2.2.1. Пусть G - сеть с М вершинами Vi, v, . . ., Vja N

ребрами. Тогда

Доказательство теоремы немедленно следует из того, что каждое ребро добавляет 1 к степени каждой из его двух вершин и поэтому добавляет 2 к сумме степеней всех вершин.

Следствие 2.2.1. В каждой сети G число вершин нечетной степени четно.

Доказательство этого следствия оставляется читателю в качестве упражнения.

Как пример использования следствия 2.2.1 рассмотрим группу из k человек, которую мы представим k вершинами V={vi, Vz, . . ., v}. Если два человека vi и vj знакомы друг с другом, то будем говорить, что для них существует ребро (vt, vj). Из следствия 2.2.1 следует, что в любой группе число людей, которые знакомы с нечетным числом других людей, четно.

Сеть G={]/, Е) является подсетью сети G={V, Е), если l/sV и ЕЕ. Если V = V, то говорят, что С- остовная подсеть G. Если vV, то G-V обозначает подсеть, вершины которой есть V-{v}, а ребра - все ребра в Е, не инцидентные v, т. е. G-v получается из G вычеркиванием v и всех инцидентных v ребер. Аналогично для ребра е={и, v) Е, G-е обозначает подсеть, получаемую из G удалением е, но не и и и; G+e обозначает подсеть, получаемую добавлением е к G.

Маршрут в сети G={V, Е) из вершины ut в вершину Un - это (конечная) последовательность вершин W=Ui, и, . , Un, таких что (Wi, a,4.i)£(G) для каждого t, lin-1. Маршрут W замкнут, если "i=Wn; в противном случае маршрут W открыт. Маршрут называется путем, если ни одна вершина (и, следовательно, ни одно из ребер) не появляется в W более одного раза. Цикл - это замкнутый маршрут til, tiz, . . ., Un, Ui, для которого UiUj, если i=7/. Рис. 2.2.6 иллюстрирует введенные термины.

Сеть G связная тогда и только тогда, когда для любых двух вершин м и D из G существует путь из « в v; в противном случае говорят, что G несвязная. В несвязной сети G максимальные связные подсети называются компонентами G.

Некоторые связные сети можно сделать несвязными, удалив одну-единственную вершину или ребро. Говорят, что вершина v является разделяющей вершиной сети G, если у G-v больше компонент, чаи У G. Ребро е является мостом в G, если у G-е больше компонент, чем у G. На рис. 2.2.6 w - разделяющая вершина и {w, у) - мост.

Теорема 2.2.2. Ребро е связной сети G является мостом тогда и только тогда, когда сушествуют две вершины Vi и v, такие, что е принадлежит каждому пути из Vt в Cg.