Lex.

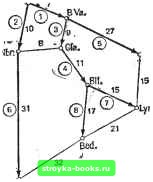АшЬ.

Poa.

Рис. 6.2.3. Дерево кратчайших путей с корнем в LEX.

всех V0.

вершин и в G; set

стояние от LEX до BED, нам пришлось вычислить кратчайшие пути от LEX до всех остальных вершин. Итак, в наихудшем случае задача отыскания кратчайшего расстояния от начальной вершины до конечной имеет ту же сложность, что и задача отыскания кратчайших путей из начальной вершины во все остальные вершины.

Теперь мы готовы к тому, чтобы сформулировать алгоритм Дейкстры для отыскания кратчайшего пути.

Algorithm DIJKSTRA для определения кратчайшего расстояния D1ST(W?) от заданной начальной вершины V0 до конечной вершины W в связной сети G с положительными весами, имеющей М вершин и ребер и представленной матрицей смежности А. Шаг 0. [Помечаем все вершины] Помечаем V0 как «определенная»; and помечаем все остальные вершины как «неопределенная». Шаг 1. [Инициализация переменных] Set D1ST (U) ч- А (V0, V) для DIST (V0) 0; and set NEXT -е Шаг 2. [Цикл] While ШXTфW do through, шаг 4 od; and STOP. Шаг 3. [Обновление кратчайшего расстояния до «неопределенной» вершины] Для каждой «неопределенной» вершины и set DIST (t/) ч-меньшее из Т)Ш {U) и DIST(NEXT)+Л(NEXT, U). Шаг 4. [Выбор кратчайшего расстояния до «неопределенной» вершины] Пусть U - неопределенная вершина, для которой расстояние DIST(t/) - наименьшее среди всех «неопределенных» вершин; помечаем U «определенная»; and set NEXT U.

Доказательство правильности алгоритма DIJKSTRA можно провести по индукции. .

Теорема 6.2.1. Алгоритм DIJKSTRA находит кратчайшее расстояние от V0 до W.

Доказательство. Мы докажем по индукции, что после п повторений шагов 3 и 4 для каждой вершины V, помеченной алгоритмом как «определенная», DIST (У) равно длине кратчайшего пути отУОдоУ. Мы также покажем, что для каждой «неопределенной» вершины U DIST (t/) есть длина кратчайшего пути от V0 до U, в котором все вершины определенные, кроме U.

Для п=0 после выполнения шагов О и 1 существует только одна определенная вершина, т. е. V0, а DISTVO)=0, очевидно, есть длина

кратчайшего пути от V0 до нее же. Кроме того, для любой «неопределенной» вершины и расстояние DIST(t/), очевидно, определяется ребром между V0 и и, т. е. путем с двумя вершинами, только одна из которых и «неопределенная».

Предположим, что теорема верна для п повторений, и предположим, что происходит (п+1)-е выполнение шага 3. Требуется показать, что для всех «неопределенных» вершин U величина DIST{t/) есть длина кратчайшего пути от V0 до U, в котором «определена» каждая вершина, кроме и.

Предположим, что это не так, т. е. что существует «неопределенная» вершина U и путь Р от V0 до U, в котором U - единственная «неопределенная» вершина, а длина Р, скажем т, удовлетворяет неравенству m<DIST(f/). Пусть У - «определенная» вершина в пути Р, соседняя с и. Если УфКЕХТ, то по предположению индукции значение DIST(6) было «определено» после п-го повторения и m=DIST(6). Это противоречит нашему предположению, что т<В15Т(У). С другой

SUBROUTINE DIJKST (A.M.V0,W,FROH,TO,LENGTH,EDGES)

С ЭТА ПОЛПРОГРАМНА ОПРЕДЕЛЯЕТ КРАТЧАЙШЕЕ РАССТОЯНИЕ ОТ

С НАЧАЛЬНОЙ ВЕРШИНЫ \р сО КОНЕЧНОЙ ВЕРШИНЫ W В СВЯЗНОЙ

С- СЕТИ G С НЕОТРИЦАТЕЛЬНЫМИ БЕСАМИ С ПОМОЩЬЮ АЛГОРИТМА,

С ПРИНАДЛЕКАЩЕГО ЛИЙКСТРЕ (NUHERISCHE: KATHEMATIC.V 1.

С 269-271). ДАННАЯ РЕАЛИЗАЦИЯ ЯВЛЯЕТСЯ ВАРИАНТОМ ПРОГ-

С РАНМЫ,ПРИНАДЛЕЖАЩИМ КИВИНУ И УИТНИ (СОНМ.АСМ (АПРЕЛЬ

С 1972).АЛГОРИТМ 422}, РЕЗУЛЬТАТОМ РАБОТЫ ЭТОЙ ПОДПРОГ-

С рАММЫ ЯВЛЯЕТСЯ ДЕРЕВО КРАТЧАЙШИХ ПУТЕЙ С КОРНЕМ V0. С

с ==я ФОРМАЛЬНЫЕ ПАРАМЕТРЫ С

с A(J,JJ ДЛИНА РЕБРА , СОЕДИНЯЮЩЕГО ВЕРШИНЫ J И J ,

С ЕСЛИ РЕБРО ОТСУТСТВУЕТ , ТО.

С Я(1 ,J) = .1 ООО ООО ,

С ПРОИЗВОЛЬНОМУ БОЛЬШОМУ ЧИСЛУ.

с VC НАЧАЛЬНАЯ ВЕРШИНА

С W КОНЕЧНАЯ ВЕРШИНА

с и ВЕРШИНЫ В G рРОНУНЕРОВАНЫ 1......Н,

С ГДЕ- 2.UE.H.UE.100

с FnOM(l) СОЛЕРШТ 1-Е РЕБРО В ДЕРЕВЕ КРАТЧАЙШИХ

С Т0(1 ГУТЕ0 от ВЕРШИНЫ =FROM( 11= К ВЕРШИНЕ

С LENGTHdl =то( 1)= ДЛИНЫ e.LENGTH{l)=.

с EDGES число РЕБЕР В ДЕРЕВЕ КРАТЧАЙШИХ ПУТЕЙ.

С НА ДАННЫЙ МОМЕНТ

Рис. 6.2.4. Реализация алгоритма DIJKSTRA.

i ВНУТРЕННИЕ ПЕРЕМЕННЫЕ

CIST(I)

NEXT

КРАТЧАЙШЕЕ РАССТОЯНИЕ ОТ UNDETIDB ЧАСТИЧНОГО ДЕРЕВА КРАТЧАЙШИХ ПУТЕЙ

ОЧЕРЕДНАЯ ВЕРШИНА КРАТЧАЙШИХ ПУТЕЙ

ДОБАВ;!ЯЕНАЯ К ДЕРЕВУ

ЧИСЛО НЕОПРЕДЕЛЕННЙХ ВЕРШИН

UNDETtI) СПИСОК НЕОПРЕДЕЛЕННЫХ ВЕРШИН

VERTEXtl) ВЕРШИНЫ ЧАСТИЧНОГО ДЕРЕВА КРАТЧАЙШИХ - ПУТЕЙ, ЛЕИАШИЕ НА КРАТЧАЙШЕМ ПУТ11 ОТ UNDETtI) ДО V0.

INTEGER AdOO.lOO),H,W,W,FnOH{100j,TO{100),LENGTH(10D) INTEGER EDGES,DIST(1tlO),NEXT,NUHUN,U№ET{100J JNTECER VERTEXllOO)

ИНИЦИАЛИЗАЦИЯ ПЕРЕМЕННЫХ

СЕНОВЯЕНИЕ КРАТЧАМЕГО РАССТОЯНИЯ ДО ВСЕХ НЕОПРЕДЕ-ДЕННЬ1Х ВЕРШИН

гсоБО зос I -i.NUHUH 1 м-г

J»UNDET(I) N (М-2){М-1)/2

JK в L + A(NEXT,J) N {H-2)(H-11/2

«F(DIST{I) .LE. JK) GO TO 300 N.A (H-2)(H-11/2.E

VERTEX(l) « NEXT Б F

EIST(I) » OK В F

ЗЙЙCONTINUE ,,, V , (к-глм-и/з

Рис. 6.2.4. Продолжение