место опыт с конечным числом равновероятных случайных значений. Кроме того, она находит применение при расчетах надежности.

Биномиальное распределение.

Модель. При схеме опыта Бернулли возможны два взаимоисключающих исхода - А и А (например, пробой или отсутствие пробоя), которые появляются с вероятностями Р(А)=р и P{A) = q{p + q=l). Биномиальное распределение задает.ска-кой вероятностью в п независимых опытах событие А возникнет ровно k раз. Рассмотрим для наглядности несколько случаев:

при п--=1 P{k=l) = p, I

Pik = 0)=l~p=q,]P + -

при п=2 P{k=2) = P(Ar\A) = p\

Р (fe = 1) = Р [(Л П Л) + (Л П Л)] = 2pq, {p+qr=l;

P(fe = 0) = P(ЛnЛ) = 9

при rt = 3 (p + qf=l,

при n = 4 {p-{-q)"= 1.

Для неизменного п и заданной вероятности появления k событий (fe<rt) сказанное можно обобщить с помощью биномиальных коэффициентов

п\ и (и - 1) . . (и - fe + 1)

fe! (и -fe)! 1-2 ... fe

Значения вероятностей (функция плотности):

P(X = fe) = ( ]р*(1-р)«Л fe = 0, 1, 2, . . ., п. (1.54) Суммарная вероятность (функция распределения):

p(x<fe)=i:f" )р"(1-р)"-«. (1.55)

т=о \ пг /

Параметры: п (число рассматриваемых случаев); р (вероятность появления Л).

Математическое ожидание:

ЕХ = пр. (1.56)

Рис. 1.10. Биномиальное распределение с параметрами р= =0,2 и ,1=10

Р(Х=к) = Ь(к п; р) - вероятности реализаций; P(X<k) = B(k; п; р) - ступенчатая функция распределения

Дисперсия: DX = np(\-p).

1,0 0,9

0,8 0,7 -0,В 0,5 0,4 0,3 0,2 -0,1

1Ъ,В

0 1 2 3 4 5 6 7 8 9

(1.57)

Пример: рис. 1.10. Таблицы [27, табл. 1А IB] имеются для единичных и суммарных вероятностей при n=l-f-25.

Точечные оценки для р. В качестве точечной оценки параметра р (вероятности) используют относительную частость hn=kfn [см. формулу (1.1)], с которой k раз появилось событие А.

Доверительная оценка для р:

1. С помощью -распределения (см. п. 1.3.2) получаем односторонний доверительный интервал с верхней границей

(k+l)F,

m,; mi; е

n-k+(k+ 1) F

(1.58)

где im,;- квантиль i-распределения порядка q==e (е -доверительная вероятность); mi = 2{k+l) и m2=2{h-k)-число степеней свободы; / = [0; Рв]. Односторонний доверительный интервал с нижней границей

k+{n - k+l)F

m,; т.; е

где тз=2{п-к+1); т=2к; 1=[рв, 1].

2. Двухсторонние доверительные интервалы табулированы Нейманом [27, табл. 1С] для л, равного 1...30. Для больших п выполняется асимптотическое соотношение

1 =-L f)fe + iL:Я,д/A(l+- I п + Х1 V 2 « V п А J

(1.60)

где А,д -квантиль нормированного нормального распределения (см. п. 1.3.2) порядка q={\-\-e)f2.

См. примечание перев. на стр. 38.

Рис. 1.11. Доверительные нижняя Рн и верхняя Рв границы неизвестных вероятностей в зависимости от относительной частости в выборке Л„ прн доверительной вероятности е=0,95 [27, табл. 1CI

Эти доверительные интервалы изображены графически на рис. 1.11. Они пригодны к непосредственному использованию.

Пример 1.16. При испытаниях постоянным напряжением в п=100 опытах зарегистрировано k=20 пробоев. Вероятность пробоя р следует оценивать как параметр биномиального распределения.

1. Точечная оценка согласно формуле (1.1): ft„=20/100=0,2.

2. Доверительная оценка с помощью F-распределення (при е= =0,95)-см. выражения (1.58) н (1.59):

числа степеней свободы: mi = =42, Ш2=160, тз=162, т4=40;

квантили: Fz, leo, o,9S= 1,47;

162, 40. 0,95= 1,56;

односторонний доверительный интервал с верхней границей /= = [0; 0,278];

односторонний доверительный интервал с нижней границей /= = [0,137; 1].

3. Доверительный интервал по Нейману (е=0,95): нз рнс. 1.11 следует, что двухсторонний доверительный интервал /=[0,13; 0,29]; тот же результат дает уравнение (1.60).

Применение. Биномиальное распределение возникнет во всех задачах испытательной техники, когда имеются явления типа «да - нет» и объем выборки мал в отличие от генеральной совокупности(Если делать выборку из генеральной совокупности, то необходимо возвратиться к использовавшемуся гипергеометрическому распределению.) Особенно важным является применение биномиального распределения в испытаниях постоянным напряжением с альтернативной постановкой вопроса (пример 1.1 и § 2.2) при оценке стандартными методами (см. гл. 3). При выполнении опытов, кото1)ые можно повторять сколько угодно раз, генеральная совокупность бесконечна.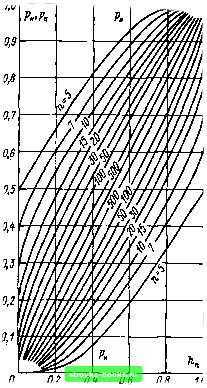

Распределение будет в точности биномиальным, если генеральная совокупность полностью независима от выполняемых опытов, т. е. если объекты сделанных опытов возвращают обратно в генеральную совокупность или если она бесконечно велика.