
 |
|
Главная Электронные вольтметры [0] [1] [2] [ 3 ] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] Получение правильного результата Перейдем к экспериментальному способу получения правильного результата при измерении напряжений вольтметрами с недостаточно высокими входными сопротивлениями. Он не требует знания параметров цепи, а расчеты сводятся к минимуму. Обратимся вновь к активному двухполюснику, который был изображен иа рис. 1. Мы имеем две неизвестные величины - интересующее нас напряжение холостого хода Ux и входное сопротивление двухполюсников /?вн- Чтобы их найти, нужно располагать двумя уравнениями. Их мы получим, измеряя напряжение поочередно двумя вольтметрами с различными входными сопротивлениями. Пусть входное сопротивление первого вольтметра Rxl, второго /?вх2. а их показания равны соответственно U\ и U. Тогда Т, т, ВХ1 . Reus RbH + BXl RuH + BX2 Из совместного решения этих уравнений получим: (RnKl-RBX2)UlU2 BXl -RaKzUi Предполагается, что /?bxi>dx2 ; реальный порядок подключения вольтметров не играет роли, поскольку индексация величин - дело условное и мы индекс 1 будем приписывать большему из сопротивлений и большему из показаний (хотя в принципе ничего не изменится от обратного, ибо одновременно сменятся знаки в числителе и знаменателе). Обозначим отношение Rexi/Rbx2 через Q(Q>1) и перепишем предыдущее выражение в более удобном для дальнейшего использования виде: На практике нет нужды в двух вольтметрах, достаточно одного. Он может быть многопредельным или же однопредельным. Очевидно, что многопредельный вольтметр прямо заменяет в данном эксперименте два вольтметра, если только его входное сопротивление различно на разных пределах измерения. Это имеет место у большинства электромеханических приборов (и части транзисторных и ламповых), у которых ток полного отклонения на всех пределах измерения один и тот же. В этом случае величина Q представляет собой не что иное, как кратность шкал, используемых для измерения. Это сразу все упрощает. Пусть, например, ампервольтметр Ц-315 на пределе измерения 100 в показывает 28 е, а на пределе 28 в его показания 20 е. Чему равно напряжение в отсутствие вольтметра? Найдем кратность Q : Q= 100/25=4. Подставляя в фор.мулу (И) числовые значения, получим: f/ = 3-28-20/(4-20 -28) = 32,3в. На рис. 4 приведена номограмма, вычерченная для формулы (И). Слева расположена ось напряжений с двумя шкалами (поль- зуются той, которая в данный момент удобнее), справа шкала Q, между ними - две наклонные вспомогательные шкалы / и . Порядок действий таков. На шкале напряжений берем точку, соответствующую большему напряжению Ui, и соединяем ее прямой с нужным значением Q на правой шкале. Точку пересечения этой Схема т/цзобанин 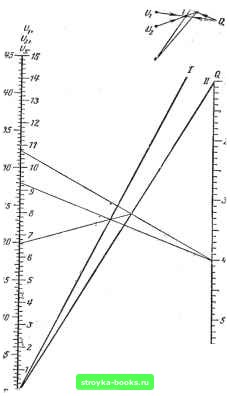 Пример Даьо:и,=28в, Ci=f, Доходим: Uj.=3Z& . Рис. 4 Номограмма для расчета действительного напряжения по результатам двух измерений. прямой с немой шкалой / соединяем с точкой на шкале напряжений, соответствующей меньшему напряжению t/2, и, продолжая эту линию, отмечаем точку ее пересечения с немой шкалой . Теперь остается провести прямую линию, которая соединит значение Q с найденной на шкале точкой, и прочитать ответ на пересечении этой линии со шкалой напряжений. На номограмме изображена дли примера схема решения предыдущей задачи (171=28 е, 2=20 е, (Q==4, отвег 32,3 в). Изложенный метод получения действительного напряжения прост и удобен. Вы подключаете свой многопредельный прибор (тестер, авометр), замечаете Показания на одном пределе, затем на другом. Берете номограмму, три движения линейки - и ответ готов. Величина Q - это отношение пределов измерения. Сами пределы по возможности выбираются так, чтобы меньшее показание U2 располагалось во второй половине шкалы. Напряжение Ux мы получаем с погрешностью, которая в основном определяется погрешностью измерения большего напряжения Ui (ее доля в общей погрешности примерно в раз превышает долю погрешности измерения U2): U2 Q где dUx и NJi-относительные погрешности измерения напряжений Ux и Ui. Если вольтметр однопредельный, то для получения второго показания U2 параллельно, вольтметру подключают резистор известного сопротивления Ri, в результате чего сопротивление вольтметра уменьшается и становится равным RbxlRiKRb}!.!+Ri)- Оно соответствует сопротивлению Rbx2 предыдущего случая, так что теперь R 1 Q = 1 + - • Порядок расчета при помощи формулы или номо-Ri граммы не меняется. При относительно высоком сопротивлении вольтметра, когда параллельное подключение -резистора с таким же сопротивлением, что у вольтметра (Q=2), вызывает лишь небольшие изменения показаний, в 5-10% от начального Ui, поправка к показанию Ui довольно точно равна самому изменению показаний вольтметра А U= = U\ - t/2, так что Ux~Ur AU. (13) И действительно, при уменьшении входного сопротивления вольтметра вдвое (Q=2) ток через него увеличивается также примерно вдвое и вдвое увеличивается падение напряжения иа внутреннем сопротивлении испытуемой цепи. Следовательно, уменьшение показываемого напряжения AU=Ui - U2, если его удвоить и приплюсовать к U2, даст действительное напряжение источника Uxk2A.U+ + U2=Ui+ А и. Но это частный случай. Точное значение поправки при любом соотношении между сопротивлением вольтметра и внутренним сопротивлением испытуемой цепи выражается через уменьшение ли показаний вольтметра при параллельном присоединении к нему любого сопротивления (любое Q) следующим образом: 1 - Ux = Ui + AVn. (15) [0] [1] [2] [ 3 ] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] 0.0011 |