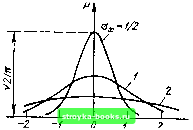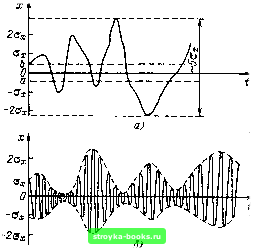Рис. 4.7. Одномерная плотность вероятности нормального распределения

Рис. 4.8. Случайные функции с одинаковым распределением (нормальным), но с различными частотными спектрами

жением свободных электронов в проводниках электрической цепи или дробовым эффектом в электронных приборах (см. § 7.3). Не только шумы и гю-мехи, но и полезные сигналы, являющиеся сум.мой большого числа независимых случайных элементарных сигналов, например гармонических колебаний со случайной фазой или амплитудой, часто можно трактовать как гаус-совские случайные процессы.

На основе функции р [х) можно найти относительное время пребывания сигнала х (t) в определенном интервале уровней, отношение макснмаль ных значений к среднеквадратическому (пикфактор) и ряд других важных для практики параметров случайного сигнала. Поясним это на примере одной из реализаций гауссовского процесса, изображенной на рис. 4.8, а для = 0. Эта функция времени соответствует шумовой по.мехе, энергетический спектр которой простирается от нулевой частоты до некоторой граничной частоты. Вероятность пребывания значения х (t) в интервале от а до b определяется выражением (4.1). Подставляя в это выражение (4.28), при = О получаем

Р{а<х<Ь)

У In Од. .

1 Ге--2а

dx=-

Угла, .

2л, J

У2л J

(4.29)

Функция Ф{и)

У2л.

(4.30)

называется интегралом вероятностей. В математических справочниках приводятся таблицы этой функции.

Таблица 4.1

Подставив в (4.29) ii/a, 1, 2, 3 и соответственно aia -1, -2, и -3, нетрудно найти вероятности пребывания х (t) в полосах шириной 2а;, 4СТя: и 6<Ух, симметричных относительно оси /. .

В рассматриваемом частном случае (а = Ь) формулу (4.29) можно упростить на основании симметрии функции относительно оси ординат (рис. 4.7).

Таким образом,

Р(-&<<6)=2

2сгг/ = 2Ф

Результаты вычислений сведены в табл. 4.1. В последней графе приведены величины, равные 1 - 2Ф {Ыа. Из этой таблицы следует, что ширину шумовой дорожки (рис. 4.8, а) нормального шума можно приравнять (4 ... 5) Ох- Если принимать во внимание пики функции х (t), вероятность которых не менее 1 %, то пикфактор шума (отношение пика к а) можно оценить значением ~3. Напомним, что для гармонического колебания пикфактор равен ]/2.

Отношение времени пребывания х (t) в заданном интервале к общему времени наблюдения (достаточно большому для эффективного усреднения) можно трактовать как вероятность попадания х (t) в указанный интервал. На такой трактовке основан принцип построения различных приборов, используемых для экспериментального нахождения одномерной плотности вероятности случайного процесса.

Можно отметить, что приведенные выше данные о распределении вероятностей не дают никаких представлений о поведении функции х (/) во времени. На рис. 4.8, б показана реализация гауссовского процесса со спектром, сосредоточенным в узкой полосе частот с центральной частотой mq. По своей плотности вероятности р (х) и, следовательно, по значениям Шх и Ох этот процесс не отличается от низкочастотного, показанного на рис. 4.8, а.

Для описания временных характеристик функции х (t) необходимо привлечь двумерную плотность вероятности, позволяющую найти ковариационную функцию [см. (4.7)1. Другой способ - нахождение спектра мощности случайного процесса. Он рассматривается в следующем параграфе.

4.3. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ МОЩНОСТИ СЛУЧАЙНОГО ПРОЦЕССА

Подразумевая под случайным процессом множество (анса.мбль) функций времени, необходимо иметь в виду, что функциям, имеющим различную форму, соответствуют различные спектральные характеристики. Усреднение комплексной спектральной плотности, введенной в §2.6 или 2.1, по всем функциям приводит к нулевому спектру процесса (при М [х (t)] = 0) из-за

случайности и независимости фаз спектральных составляющих в различных реализащ1ях. Можно, однако, ввести понятие спектральной плотности среднего квадрата случайной функции, поскольку значение среднего квадрата не зависит от соотношения фаз суммируемых гармоник. Если под случайной функцией X (t) подразумевается электрическое напряжение или ток, то средний квадрат этой функции можно рассматривать как среднюю мощность, выделяемую в сопротивлении 1 Ом. Эта мощность распределена по частотам в некоторой полосе, зависящей от механизма образования случайного процесса. Спектральная плотность средней мощности представляет собой среднюю мощность, приходящуюся на 1 Гц при заданной частоте м. Размерность функции W (м), являющейся отношением мощности к полосе ч астот, есть

Мощность

Полоса частот

= [МощностьX время] -[Энергия].

Спектральную плотность случайного процесса можно найти, если известен механизм образования случайного процесса. Применительно к шумам, связанным с атомистической структурой материи и электричества, эта задача будет рассмотрена в § 7.3. Здесь же мы ограничимся несколькими определениями общего характера.

Выделив из ансамбля какую-либо реализацию (t) и ограничив ее длительность конечным интервалом Т, можно применить к ней обычное преобразование Фурье и на!йти спектральную плотность Хг («). Тогда энергию рассматриваелюго отрезка реализации можно вычислить с помощью формулы (2.66):

г/2 оо

Э,г- f х1т(()Ш.-~ J jXHaNw. (4.31)

- 7/2 - оо

Разделив эту энергию на Т, получим среднюю мощность /г-й реализации на отрезке Т

х1т it) - "У da. (4.32)

- оо

При увеличении Т энергия Эг возрастает, однако отношение Эт IT стремится к некоторому пределу. Совершив предельный переход Т-оо, получим

2л J 7--*ос Т 2л J

- СО

X.,., (О)) [2 7-сое Т

W,(co). lim-i (4.33)

представляет собой спектральную плотность средней мощности рассматриваемой k-n реализации.

В общем случае величина Wu («») должна быть усреднена по множеству реализаций. Ограничиваясь в данном случае рассмотрением стационарного и эргодического процесса, можно считать, что найденная усреднением по одной реализации функция (а) характеризует весь процесс в целом. Опу-