Далее по формуле (2.9) с учетом (3.116)

со со

"=-,7-4-. f А(Оф„(0==Д/о f A(t)>n(t)dt. (3.117)

фп1Г J J

Используя формулу (2.63), в которой заменяем © на Q\ получаем

- ди)о/2 д(оо/2

=-fo-~ f 8.4(У)-е"Д«Л2=А(пА0=Л(пД0ее("АО. (3.118)

-Ао)„/2 °

В выражении (3.118) 8л - спектр комплексной огибающей A{t), а А (nAt) - ее значение в отсчетной точке t = nAt.

Итак, коэффициенты ряда (3.110) являются выборками функции A{t), взятыми через интервалы At = 1/А/о-

Подставляя (3.118) в (3.111), получаем

г„(0-= 1] Л(пД0ф„(0е»+<" и по формуле (3.112) определяем

а(0= V Л(пАОфЛОсо5[©о/ + е(пАО]-

У А (nAt) cosK?-fe(nA01. (3.119)

п= - оо

При заданной длительности сигнала Т. число отсчетных точек TJAt = = ТрА/о, причем в каждой точке должны быть заданы два параметра: А {nAt) и 6 (nAt).

Следует иметь в виду, что при несимметричном (в полосе А ©о) спектре введенная в данном параграфе частота ©о = (©j + ©2)/2 .может не совпадать со «средней частотой» в выражении (3.73). Иными словами, фаза 6 {t) может содержать слагаемое, линейно-зависящее от времени.

Проиллюстрируем выражение (3.119) на примерах колебания, промоду-лированного по амплитуде или по частоте.

При AM исходим из колебания а (t) ~ А (t) cos (ot, в котором А (t) - вещественная функция со спектром $а (©), ограниченным наивысшей частотой Qm = Рт- В ЭТОМ случае ширина спектра модулированного колебания а (t) равна А/ам = 2/™, причем в пределах этой полосы спектральная плотность Sa (©) симмстрична относительно ©0. Интервал между выборками в соответствии с формулой (3.113) должен быть не больше чем At = = 1/А/ам = l/2.Fm, т. е. таким же, как и при дискретизации исходного сообщения (модулирующего напряжения).

Так как фаза высокочастотного заполнения при чисто амплитудной модуляции постоянна, то передавать ее нет необходимости. Отсюда вытекает очевидный результат: амплитудио-модулированное колебание вполне определяется значениями своих амплитуд, взятыми через интервал \/2F,n, где Рт - верхняя частота в спектре модулирующей функции (т. е. в спектре передаваемого сообщения).

1 Поскольку здесь рассматривается сректр огибающей.

Иными словами, при чисто амплитудной модулящш число степеней свободы модулированного колебания такое же, как и число степеней свободы модулирующей функции.

Рассмотрим теперь частотно-модулированное колебание

a{t) = Ад cos [©0+0 (01. когда мгновенная частота со (f) = ©о + dQIdt модулирована тем же сообщением, что и в предыдущем случае, причем максимальная девиация частоты /д велика по сравнению с F, так что ширину Д/, полосы частот модулированного колебания можно приравнять к 2/д [см. случай «широкополосной» частотной модуляции, (3.34)]. Интервал между выборками должен быть взят At < УА[,, = 1/2/д. Так как при ЧМ амплитуда колебания неизменна, то передавать ее нет необходимости. Следовательно, для однозначного представления частотно-модулированного колебания достаточно задавать фазу 6 (nAt) этого колебания в отсчетных точках, отстоящих одна от другой на время At < 1/2/д. При одной и той же длительности сообщения число выборок фазы при ЧМ A/jT, = 2/д7р, а число выборок огибающей при AM А/амТс == РтТс- Отсюда видно, что при одинаковом передаваемом сообщении (при одинаковом количестве информации) частотно-модулированный сигнал обладает числом степеней свободы в /„/f = т раз большим, чем амплитудно-модулированный. Это является результатом расширения спектра сигнала при ЧМ. На приемной стороне канала связи после частотного детектирования модулированного колебания выделяется напряжение, которое имеет спектр и число степеней свободы такие же, как и исходное сообщение.

Из приведенного примера следует, что при одной и той же ширине спектра информационная емкость радиосигнала различна в зависимости от вида модуляции.

При смешанной модуляции - амплитудной и угловой - в каждой отсчетной точке нужно брать две выборки: амплитуды и фазы.

Глава 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ СИГНАЛОВ

4.1. ОБЩИЕ ОПРЕДЕЛЕНИЯ

Информация, передаваемая по каналу связи или извлекаемая в результате измерения, заключена в сигнале.

До приема сообщения (до испытания) сигнал следует рассматривать как случайный процесс, представляющий собой совокупность (ансамбль) функций времени, подчиняющихся некоторой общей для них статистической закономерности. Одна из этих функций, ставшая полностью известной после приема сообщения, называется реализацией случайного процесса. Эта реализация является уже не случайной, а детерминированной функцией времени.

Важной, но не исчерпывающей характеристикой случайного процесса является присущий ему одномерный закон распределения вероятностей.

На рис. 4.1 изображена совокупность функций (t), (t), образующих случайный процесс X (t). Значения, которые могут принимать отдельные функции в момент времени t = t, образуют совокупность случайных величин Xi (t), х (t), ...

Вероятность того, что величина Xh (tl) при измерении попадает в какой-либо заданный интервал (а, h) (рис. 4.1), определяется выражением

Pi (а < л: < 6) = " р {х; t) dx.

(4.1)

Функция р {х; tl) представляет собой дифференциальный закон распределения случайной величины X (?i); ? {х\ ?]) называется одномерной плотностью вероятности, а Pt - интегральной вероятностью.

Функция р {х; tl) имеет смысл для случайных х непрерывного типа, могущих принимать любое значение в некотором интервале. При любом характере функции р{х\ ti) должно выполняться равенство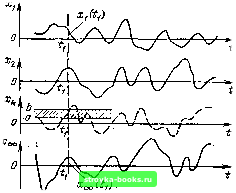

Рис. 4.1. Совокупность функций, образующих случайный процесс

\ p(x;ti)dx=l,

(4.2)

где XjTiin и -max - границы возможных значений х (tl).

Если же X является случайной величиной дискретного типа и может принимать любое из конечного числа дискретных значений, то (4.2) следует заменить суммой

(4,2)

где Р,- - вероятность, соответствующая величине Х;.

Задание одномерной плотности вероятности р (х; ti) позволяет произвести статистическое усреднение как самой величины х, так и любой функции f (х). Под статистическим усреднением подразумевается усреднение х по множеству (по ансамблю) в каком-либо «сечении» процесса, т. е. в фиксированный момент времени.

Для практических приложений наибольшее значение имеют следующие параметры случайного процесса:

математическое ожидание

т (t) = М [X (t)] = j хр (х; t) dx;

- оо

дисперсия

l\(t)=M{{x(t)-mAt)?y, среднее квадратическое отклонение

а, (О М {[X(t)-m, (t)f} = KD, (t).

(4.3)

(4.4)

(4.5)

Одномерная плотность вероятности недостаточна для полного описания процесса, так как она дает вероятностнре представление о случайном процессе X (t) только в отдельные фиксированные моменты времени. Более