в, (т) = - Г (©) е» do3 = 4 - С SI (ш) е» = 2л J 2л J

2л J

So (<u) COS шхйш -f /4

So (со) sin coTdco.

(3.95)

Действительная часть этого выражения есть не что иное, как удвоенная корреляционная функция исходного физического колебания а (/), т. е. 25а (т), а мнимая часть учитывает взаимную корреляцию колебаний а (t) и a,{t).

Для раскрытия смысла мнимой части выражения (3.95) вернемся к общему определению корреляционной функции (3.94) и запишем ее в форме

fiz(T)-= J la{t) + iai{t)][a(t-\-x)~iai{t+x)]dt

a{t)a{t + i)dt+ j ai(t}ai{i + x)dt + i

j ai(t)a{t + x)dt -

j a{t)ai(t + x)

B, (T) + (t) + / [B,.a ir)-B,a, (T)]. (3.95)

В §2.19 было установлено, что корреляционная функция действительного сигнала зависит только от модуля спектральной плотности. Так как модули спектров функций а (t) и Oj (t) одинаковы (см. § 3.9), то первые два интеграла в (3.95) равны и в сумме дают 2Б„ (т). Следовательно, мнимые части в выражениях (3.95), (3.95) совпадают и можно написать следующее равенство:

В„.Лт)-В„„,(т)-4 J Sl(co) sin coTcioj.

Но в соответствии с (2.137) Ваа, (х) = Ваа (-т), ТЭК ЧТО левую часть можно записать в форме Ва (т) - Аа.а {-х). Далее, правая часть, содержащая под интегралом множитель sin сот, является нечетной функцией т, откуда следует, что и разность Sa.aW - Ват W является нечетной функцией. Это возможно только при нечетности функции Ваа (т). Таким образом, приходим к равенству В„,а (т) - (т) = 25, (т) и соответственно к соотношению

B,;,a(T)«2-i- Г S?,(0))sinC0TdT.

2 л J

Формулу (3.95) теперь можно представить в виде

B,(T) = 2B„(T) + i2fi„,„(t). (3.96)

Итак, Re \В (т) = 2В„ (т), откуда вытекает полезное соотношение между корреляционной функцией Ва (т) исходного действительного сигнала и корреляционной функцией В, (т) аналитического сигнала

Ва(х)Я\ВАх)\.

(3.97)

4. Корреляционные функции аналитического сигнала и комплексной огибаюш,ей этого сигнала связаны между собой соотношением

В,(х) Ва(х). (3.98)

Действительно, подставив в (3.94) г, (t) = \{t) е"« иг; {t)=\* (О X X е-"», получим важное соотношение

a(t)

art)

(T) = e-"»

+ T)d

A (0 A* {t 4-(3.99)

Рис. 3.29. Формирование аналитического сигнала, соответствующего заданному вещественному сигналу a(t)

В котором интеграл есть корреляционная функция комплексной огибающей \{t). Поэтому выражение (3.97) можно записать в форме

В„ (т) - Re [е-« Вл (т) = -Re В частности, при т = О получаем

Ва(0)-у j лО--уВг(о).

е-">.т J А(/) А*(/ + т)Л

. (3.97)

(3.100)

Из этого выражения видно, что, поскольку В (0) = Э, энергия аналитического сигнала равна удвоенной энергии исходного действительного сигнала.

Следует указать, что применение понятия энергии к комплексной функции имеет не только формальный смысл. В гл. 13 будет показано, что в некоторых устройствах обработки сигналов приходится иметь дело с совокупностью двух функций времени, сопряженных по Гильберту, т. е. с аналитическим сигналом как .с физическим процессом.

Формирование аналитического сигнала можно пояснить на простой модели, показанной на рис. 3.29. Исходный сигнал а (t) = А (t) cos («о/ + + 0 (01 подается на выход непосредственно по прямому каналу и через фазосдвигающее устройство, обеспечивающее сдвиг на -90° для всех спек-трльцых составляющих узкополосного сигнала а (t). В результате такого сдвига получается колебание А (t) cos [©q + 9 (О - 90°] = А (t) sin [at + + 0 (/)] = Qi (t), сопряженное no Гильберту функции a (t). Следовательно, совокупность a (t) и % (i), действующую на выходе, можно трактовать как аналитический сигнал

Za (О = А (t) е9<> е""» А (f) e"•

В последующих главах будут даны примеры применения понятия «аналитический сигнал» как для упрощения анализа прохождения через радиоцепи сигналов действительных, так и для описания совокупности двух квадратурных сигналов.

3.11. КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ МОДУЛИРОВАННОГО КОЛЕБАНИЯ

Прн нахождении корреляционной функции модулированного колебания а (t) = А (t) cos 1)5 (t) будем исходить из условия абсолютной интегрируемости функции а {t) (сигнал с конечной энергией), что позволяет применять определение (см. § 2.18)

В„ (т) = Г а (О а (1 i т) dt

(3.101)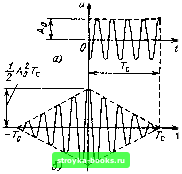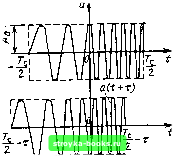

Рис. 3.30. Импульс с высокочастотным заполнением (а) и корреляционная функция (б)

Рис. 3.31. К построению корреляционной функции ЛЧМ и.мпульса

Вычисление интеграла для сложных сигналов требует громоздких выкладок. Задача существенно упрощается при переходе от колебания а (t) к аналитическому сигналу Za (0= А(?)е"«. Основываясь на соотношениях, выведенных в предыдущем параграфе, рассмотрим сначала чисто а.м-плитудную модуляцию, когда а (t) = А (t) cos «о?, 0 (?) = О и, следовательно, А(?) = А* (?) = А (?).

Тогда формула (3.97) принимает вид

Ва (T)-YRe

Л(?) л (? + т) dt

= cos©oT j Л (?) Л (? + т) d?.

(3.102)

Обозначив, как и в выражении (3.97), интегральный множитель через Ва (т), окончательно получим

Ва (i)=Ba (т) (VaCOSCOoT).

(3.103)

Второй множитель (Va cos ©„т) есть корреляционная функция гармонического колебания с частотой ©о и единичной амплитудой.

Итак, корреляционная функция амплитудно-модулированного радив,-сигнала равна произведению корреляционных функций огибающей и высокочастотного заполнения.

В качестве примера на рис. 3.30, а показан радиоимпульс с прямоугольной огибающей, а на рис. 3.30, б - соответствующая этому импульсу корреляционная функция. Следует отметить, что эта функция не зависит от начальной фазы заполнения радиоимпульса, а ее огибающая совпадает с корреляционной функцией прямоугольного видеоимпульса (см. §2.18, рис. 2.36, г).

Для иллюстрации применения общего выражения (3.99) к амплитудно-частотной модуляции найдем корреляционную функцию импульса, изображенного на рис. 3.19, а.

При обозначениях формулы (3.37) и рис. 3.19 аналитический сигнал запишется в виде

Za (?) - Ло еЭ/2 е»о TJ2 < ? Г,/2.

(3.104)