Последовательность временных отсчетов приобретает вид последовательности дельта-функций с весовыми коэффициентами, равными значениями сигнала s (t) в точках kT (см. рис. 2.34, б).

При этом выражение (2.121) принимает вид

S7. ((.))-=- V S(o) -лш,).

(2.123)

Отметим, что энергия сигнала St (t), выраженного через дельта-функции, бесконечно велика. Соответственно и энергия спектра Sr (w), определяемого выражением (2.123), бесконечно велика. При использовании же реальных тактовых импульсов с конечной энергией спектр Sr (10) ири (О -». схэ убывает (см. рис. 2.35).

Представление sr (t) в форме (2.122) существенно упрощает спектральный анализ дискретных сигналов. Например, спектральную плотность Sr (со) можно определить непосредственно по совокупности временных отсчетов {s (kt)}, без обращения к спектру S (со) исходного континуального сигнала. Действительно, применив обычное преобразование Фурье (2.48) к выражению (2.122) для случая, когда = О, 1..... оо. получим

Sr (со) = .Sr (t) е dt=\ е -<"< V s (kT) 6 (/ kT) dt

= V s (yfe7)j e 6 (/ -kT) Л = V s [kT) e "r

(2.124)

По своей размерности! функции S (со) и Sr (со) неодинаковы: первая име-

Сигнал , ]

-- , а вторая - просто [сигнал!.

частота J

Переходя к комплексной частоте р = а Л- /со, получаем изображение

ет размерность

по Лапласу дискретизованного сигнала

Sr ip) = L \St (t)\ = V s (kT) e -

(2.125)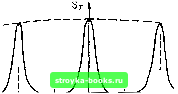

sine (ля-

-Un/T

-Zn/T -ы„ 0

Zn/T

Рис. 2.35. Спектры исхо.хного (a) и .1Искретизованного (б) сигналов «6

Оригинал, т. е. функцию Sj (/), можно определить по заданному изображению Sr (р) с помощью обратного преобразования Лапласа, записываемого в обычной форме:

<Т -i- /X

s,.{,)=.-L- Г Sr(p)ePdt (2,126)

2л/ J IcM. (2.103)1,

Выражение (2.126) определяет всю последовательность {s (кТ)} в форме, совпадающей с выражением (2.122). Для определения одного k-ro отсчета S (kf) без множителя б (t - kT) можно применить более простое выражение

S (кТ) = Т - Г S (р) dp, (2.127)

2я/ J

о, - in IT

В котором интегрирование ведется в пределах одного частного интервала от -л/Г до л Т.

Некоторые дополнительные характеристики дискретных сигналов, существенные при цифровой обработке, приводятся, в § 12.2.

2.18. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ДЕТЕРДАИНИРОВАННЫХ СИГНАЛОВ

Наряду со спектральным подходом к описанию сигналов часто на практике оказывается необходимой характерцстика, которая давала бы представление о некоторых свойствах сигнала, в частности о скорости изменения во времени, а также о длительности сигнала без разложения его на гармонические составляющие.

в качестве такой временной характеристики широко используется корреляционная функция сигнала.

Для детерминированного сигнала s (t) конечной длительности корреляционная функция определяется следующим выражением:

в, (т) = ( S (t) S* и + т) dt, (2,128)

- (V-

где т - временной сдвиг сигнала.

• Вычислим правую часть (2,126) после замены пределов интегрирования, подстановки / =- тТ, где т - любое целое число, и подстановки S (р) по формуле (2.125):

о,--/лТ 3 a,+in/T

I

о, "/лГ О О о, -/я/Г

Учитывая, что в данном случае р - а, /(о, и переходя к переменной интегрирования ы, получаем

/=V ,,т)е"-"~г± мп(т-.)л 0 , л (m-k) Т

При т = k / = S (кТ),Т, а при т к 1 = 0. Таким образом, для определения S {kT) достаточно заменить в (2,126) Sj. (/) на s (кТ) и пределы интегрирования а, -- (оо, а, - (ОО на а, - in Т. п, (л Т

3* 67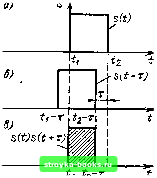

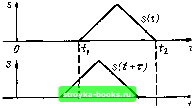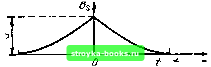Рис. 2.36. Построение корреляционной функции для прямоугольного импульса

Рис. 2.37. Построение корреляционной функции для треугольного импульса

В данной главе рассматриваются сигналы, являющиеся вещественными функциями времени, и обозначение комплексного сопряжения можно опустить:

(2.129)

Из выражения (2.129) видно, что (t) характеризует степень связи (корреляции) сигнала s (t) со своей копией, сдвинутой на величину т по оси времени. Ясно, что функция В, (t) достигает максимума при т = О, так как любой сигнал полностью коррелирован с самим собой. При этом

(2.130)

т. е. максимальное значение корреляционной функции равно энергии сигнала.

С увеличением т функция В, (т) убывает (не обязательно монотонно) и при относительном сдвиге сигналов s (/) и s (/ -f т) на время, превышающее длительность сигнала, обращается в нуль.

На рис. 2.36 показано построение корреляционной функции для простейшего сигнала в виде прямоугольного импульса (рис. 2.36, а). Сдвинутый на т (в сторону опережения) сигнал s (/ + т) показан на рис. 2.36, б, а произведение S {t) S (/ -f т) - на рис. 2.36, в. График функции В (т) изображен на рис. 2.36, г. Каждому значению т соответствуют свое произведение S (/) S (/ т) и площадь под графиком функции s (/) s (t + т). Численные значения таких площадей для соответствующих т и дают ординаты функции В,, (т).

Аналогичное построение для треугольного импульса изображено на рис. 2.37. Из общего определения корреляционной функции, а также из приведенных примеров видно, что безразлично, вправо или влево относи-