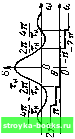<N S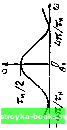

I- +?

я я о. о. с е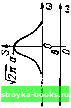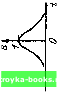

«

"I

«6

3 1

S ° 3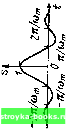

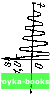Во втором примере (рис. 2.24, б) производная функции -ае-« при />0,

s (0 =

при t< О,

не содержит дельта-функции, но терпит в точке / = О разрыв. После повторного дифференцирования получим функцию, отличающуюся от исходного сигнала s (/) только масштабом по оси ординат и наличием функции -2аб (t).

Следовательно, спектральная плотность второй производной S,»(co) = aS,(co)-2a,

причем при to = О эта функция равна -а.

Разделим теперь полученное выражение на (/со) и учте.м, что Sj» (ш)/ (ш)2 есть спектральная плотность двухкратного интеграла от функции S" (t), т. е. (ш)/(ш)2 = S, (ш).

Таким образом, можно составить следующее соотношение:

S, (со) = [а S, (ш) - 2a]/(iш)

откуда вытекает равенство

S,(co) = 2a/(a + co2). При со » а Ss (со) = 2а/ш*.

Отсюда видно, что разрыв первой производной приводит к убыванию спектра по закону Этот результат можно обобщить следующим обра-

-Za -a 0\ a Za/ i

Рис. 2.24. Примеры сигна.чов:

a) с разрывом; б) с изломом; в) без разрыва и излома

зом: вне основной полосы частотный спектр убывает по закону 1 (о"+, где п-порядок производной, при котором возникает первый разрыв.

С этой точки зрения сигнал, показанный на рис. 2.24, в, производные которого непрерывны при всех значениях п, вплоть до л = оо, должен обладать спектром, скорость убывания которого является максимально возможной. Этот вывод согласуется с тем, что произведение длительность х полоса минимальна для колоколообразного импульса (см, п. 1 данного параграфа).

Основываясь на приведенных рассуждениях нетрудно также объяснить происхождение пульсации спектра вне основной полосы частот. Периодическая пульсация с неубывающими максимумами может возникать только в результате интерференции спектров двух дельта-функций, разнесенных во времени. Спектр прямоугольного импульса, пульсирующий с максимумами, убывающими по закону Г/со, является наглядным примером интерференции спектров двух единичных скачков.

2,13. СПЕКТРЫ НЕКОТОРЫХ НЕИНТЕГРИРУЕМЫХ ФУНКЦИЙ

Одним из условий применимости преобразования Фурье к функции S (t) является ее абсолютная интегрируемость:

( s(OW/< 00. (2.95)

- ос

Это условие существенно ограничивает класс сигналов, для которых существует спектр Фурье, выражаемый обычными функциями. Например, такие важные для теории сигналов и цепей функции, как гармоническое колебание, заданное при -оо <: оо или включаемое в некоторый момент времени, единичный скачок, и некоторые другие функции не отвечают условию (2.95).

Рассмотренные в предыдущем параграфе свойства дельта-функции позволяют устранить это препятствие.

Обратимся, например, к гармоническому сигналу s (t) Ад cos (со,, + -+ Оо). Не обращая внимания на то, что такой сигнал не является абсолютно интегрируемым, выражение для спектральной плотности запишел в фор.ме (2.48):

л УС

S (U)) = S (/) е dt = А„ 1 cos ((о„ С -Ь В) е - cli =

А у А p-f*" ,

I еI(<"-(.)„)( I 2±1 I е "<""»>d/.

2 ,1 2 .

На основании, формулы (2.94) получаем

S ((,)) = [2яе«*« б (о) -(Од) 4- 2яе -»»б (о) ; о,}] =

= Л„ л (е"« б (со-(о„) he б (со + w„). (2.96)

Эта функция равна нулю для всех частот, кроме го = соо и (о = -со, при которых S (со) обращается в бесконечность. Как и следовало ожидать, гармоническому колебанию с конечной амплитудой соответствует бесконечно большая спектральная плотность при дискретных частотах со„ и -со,,.