16.7. ПРИМЕР ОПРЕДЕЛЕНИЯ ЗАДЕРЖКИ СИГНАЛА

Для иллюстрации метода воспользуемся сигналом Sj (t) в виде импульса (рис. 16.15)

Si{t)=.Ate-»t, b>0,tO.

ИмпульсSi (t) достигает своего максимума при Ы = \, так что амплитуда импульса Simax = (А/Ь) Ые-* = (А/Ь) е . Спектральная плотность выбранной функции

S (ш) = А /{Ь+ (16.29)

Имея в виду цифровую обработку, переходим к дискретному времени t = тТ; тогда

Siim)=:ATme-", m-Q, 1, .... N-\,

и максимальное значение отсчета сигнала Sj {t) получается при т = \1ЬТ (см. рис. 16.15).

Перейдем от спектральной плотности (16.29) к г-преобразованию 51(е<")=ЛГ 2 /пе-"е-<"" = ЛГ те-<+<"П". (16.30)

т=0 т=0

Получилась арифметико-геометрическая прогрессия.

Шаг дискретизации Т зададим из условия, чтобы на длительность импульса приходилось достаточно большое число отсчетов N, а постоянную b - - из условия <g 1. При этом верхний предел суммирования N - 1

в выражении (16.30) можно заменить на оо, что приводит к простому результату

5(е<-0 = ЛГе-е-<-/(1 -е-e--Ol (16.31)

Модуль полученной функции Ат о~->т

Si(e«0 =--- (16.31)

1 2е-*соз(йГ + е-2*

1п I Si (е"Г) 1= = In {ATf-- 2ЬГ - 21 n (1 - 2 е- "Г cos (оТ 4- е- .

Применив к этому выражению формулу (16.20), noлyчим: при т = Q

С,1 (0) = 1 п {ATf- 26Г - 2 -i- j" 1 п (1 - 2 е - cos о)Г -f е " 2") d (юГ) =

= 1п(ЛГ)=-26Г; при тфО

(т) = -2 j In (1 - 2 е- cos (оГ -f е- 2") cos (тыТ) d (©Т) = п \ т

-2ЬтТ

1 См. [31], формулы (4.224.14), (4.397.6), 16* 483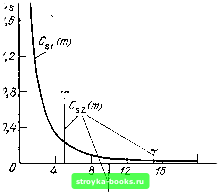

Вычислим Csi (tti) для следующе-

мкс, =0,9Ь,

го частного случая: т„ = 5 мкс, Л=

= 128, Т = T„/yVs»40 НС, е-ЬТ » 0,05, b = 1,25-10".

Кепстр Csi (fti) представлен на рис. 16.16. На том же рисунке показан кепстр Cs2 (т), соответствующий коэффициенту а == 0,8 и задержке 0 = ШоТ при /По = 5. Как видно из этого рисунка, кепстр Ci (т) концентрируется вблизи точки т = О и монотонно убывает с возрастанием т. При 0 > 5Т обеспечивается существенное превышение Cgj (т) над Csi (fti), что открывает возможность измерения весьма малых задержек даже при наличии помех. В данном примере минимальная измеряемая задержка t(, составляет всего лишь ~ 5% от длительности импульса. Для реализации такого же разрешения путем укорочения зондирующего импульса его длительность должна быть не больше ~0,25 мкс.

Сопоставим полученный результат с тем, который можно получить с помощью метода корреляционной функции. Заметим, что структурная схема, показанная на рис. 16.11, отличается от схемы рис. 12.44 только наличием операции логарифмирования. Определим корреляционную функцию сигнала S (т) = Si (т) + asi (т - т„) выражением

20 /77

Рис. 16.16. Кепстр Csi(m) сигнала Si{t), показанного на рис. 16.15 и кепстр Csiim) при а = 0,8 и задержке t„ = = то7"=5Г

Bs(m)=.

S(e«) cos (тшТ)(1{шТ).

С помощью процедуры, использованной при выводе выражений (16.25)- (16.28), нетрудно прийти к следующему результату:

ВАт) = {1+ а) 5si (т) + аВ, (т-т,) + аВ, (т + т,).

Даже при а ->. 1 и отсутствии помехи определение задержки по функции Bs (т) возможно лишь при задержках t, не меньших чем т„/2. Этот результат иллюстрирует эффект, обусловленный введением операции логарифмирования перед преобразованием Фурье.

Итак, кепстральная обработка позволяет существенно облегчить определение задержки. Однако этот выигрыш достигается весьма дорогой ценой. Требуется применение широкополосного тракта обработки с очень низким уровнем шумов, поскольку уровень спектральной плотности полезного сигнала в центральной части диапазона О, 1/Т чрезвычайно низок.

Так, при (оТ - О

Si (е") = (ATf

а на частоте шТ = л

Si(e") (ATf

,- 2bT

фТ)*

jAT) 2*

(16.32)

(16.33)

Отношение jSj (e")p/Si (e")= при 6Г = 0,05 уменьшается до (0,05/2)* л; « 4-10-" 64 дБ.

Задача существенно облегчается при использовании сигналов, спектр которых убывает пропорционально 1/со [а не 1/со, как в (16.29)1.

16.8. ВЛИЯНИЕ ПОМЕХ

Кепстральная обработка, основанная на логарифмической нелинейности, весьма чувствительна к воздействию помех. Для оценки допустимого уровня помехи рассмотрим следующую модель: входной сигнал s (t), длительность которого и спектральная плотность 5 (со) известны, действует на фоне помехи х (/), являющейся стационарным случайным процессом с заданной спектральной плотностью мощности Wx (со).

Отношение сигнал-помеха на входе устройства определим как отношение соответствующих энергий:

сигнала

5,= J 5= (со) dco; (16.34)

- ОО

помехи

Эх -Т,о1 = Т, -i- J Wx (со) dco, (16.35)

- оо

где Ох - средняя мощность помехи, которая действует на отрезке времени Тр, совпадающем с длительностью обрабатываемого сигнала s (t).

Из последнего выражения вытекает, что величина TWx (м) имеет смысл спектральной плотности энергии помехи.

Таким образом, отношение

т)(со)=52(со)/Т, «?Л(о) (16.36)

характеризует отношение спектральных плотностей энергии сигнала s (t) и помехи X (t) на входе устройства.

После дискретизации s [t) я х (t) с шагом Т функция S= (со) преобразуется в Sf (со) - 1 S (со), а Wx (со) - в Г,г (со) = \Г, (со) (см. § 2.17),

но их соотношение остается прежним, поэтому функцию т) (со), записанную в форме (16.36) или в несколько иной форме

,(o,) !l1!!L 5ИС0)

r..U.,,M ГеГ.И/Г

МОЖНО трактовать как отношение энергетических спектров сигнала и помехи на входе логарифмической нелинейности.

Для выявления взаимодействия сигнала и помехи в указанной нелинейности обратимся к структурной схеме на рис. 16.11 и допустим, что на полезный сигнал S (t) накладывается (аддитивно) одна из реализаций случайного процесса х (t).

После дискретного преобразования Фурье (на выходе БПФ) получим совокупность спектральных коэффициентов {Ут («)}, « = 0. 1. - 1,

\т(п) = 5т(п)+\т(п),

48.5