при уменьшении шага дискретизации Т до значения, малого по сравнению с т, аргумент косинуса соГ в области частот, соизмеримых с 1/т, отвечает условию соТ 1, так что cos соТ « 1 - (o)T)V2. При этом

(ThY !

/С? И

(Г/т)2 + (соГ)2 + -(соГ)2 1 + (сог)2+ - (сог)2 т т

с помощью этого выражения легко оценивать влияние Т на отклонение Кт (ю) от /Са (ю). При Tlx йС: 0,2 это выражение несущественно отличается от К1 (ю).

Обратимся к сравнению импульсных характеристик g (kT) и (О-При Т/т « 1 можно положить bl = 1/(1 -f Т/т) « (1 - Т/т) е-/-. Тогда g (kT) = aofef « ао е-*/, т. е. g (kT) отличается от g (kT) только постоянным коэффициентом (ао вместо 1/т).

Итак, для удовлетворительного совпадения характеристик цифрового и аналогового фильтров в данном примере требуется выполнение условия Т/т < 0,2.

При более сложных цепях синтез, основанный на дискретизации дифференциального уравнения, становится громоздким. Более эффективен способ синтеза цифровых фильтров по заданным полюсам и нулям передаточной функции Ко (р) аналогового прототипа на р-плоскости. Задача синтеза при этом сводится к рациональному выбору оператора преобразования р-плоскости в г-плоскость. От выбранного оператора зависят свойства и характеристики цифрового фильтра.

Наиболее простым оператором преобразования является соотношение Z = еР, использованное в гл. 12. В этом случае полюсы zm и нули Zo„ определяются равенствами

n™ = en- zo„=eo" (15.69)

Метод, основанный на операторе г = ер, иногда называют методом стандартного г-преобразования.

Выясним степень приближения характеристик синтезируемого цифрового фильтра к аналоговой модели на примере рассмотренного выше четырехполюсника (см. рис. 15.18). Передаточная функция Ка (р), определяемая выражением (15.63), имеет один полюс

р„= 1 ?С= - 1-..

Основываясь на (15.69), находим полюс на г-плоскости г„ = еп = е-/=е-«. Тогда

К z) = 1/(1 -2„ Z-1) = 1 /(1 е-г/«с 2-1),

К(е»г)= 1/(1 е-г/ е-») (15.70)

и АЧХ фильтра

IК (со)! = 1 /1/1 + е-277т 2е-г/ cos соТ. (15.71)

Далее, и.мпульсная характеристика g (kT) = е-т/х [см. (12.46)1. Замечаем, что g (kT) совпадает (с точностью до постоянного коэффициента 1/т) с импульсной характеристикой gg (t)= (Vt) е-/, дискретизованной с шагом Т, причем это совпадение не зависит от Т (в отличие от метода, основанного на дискретизации дифференциального уравнения цепи).

Аналогичный результат имеет место и для более сложных цепей.

в связи с этим метод синтеза, основанный на стандартном преобразовании Z = е"*, получил название метода, инвариантного относительно импульсной характеристики. При этом, однако, АЧХ цифрового фильтра может существенно отличаться от АЧХ аналогового прототипа, что было объяснено и проиллюстрировано в § 12.8, п. 2.

15.13. МЕТОД ИНВАРИАНТНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК

Для осуществления синтеза, инвариантного по отношению к АЧХ, следует применить преобразование, при котором бы вся мнимая ось /со р-плос-кости отображалась на г-плоскости одним обходом окружности радиуса

Этому требованию отвечает билинейное (дробно-рациональное) преобразование

г = (1 + р)/(1 -p),p=(z- 1)/(г + 1), (15.72)

где р = (ст + to))/Qo, а Qo - произвольная постоянная, обеспечивающая безразмерность величины р, выбираемая исходя из соображений нормирования.

Для уяснения смысла билинейного преобразования положим ст = О, т. е. приравняем р = ico/Qo, и на основании (15.72) запишем

= + = е< 2 arc tg u./Q. е1ф((о/о„) (15.73)

Из этого выражения следует; перемещению точки р вдоль оси /co/Qo соответствует перемещение точки г по окружности радиуса г = 1. В этом отношении билинейное преобразование не отличается от обычного г-преобразования, при котором гр=,ш = е* (см. § 12.6). Отличие в том, что угол (оГ возрастает пропорционально частоте со, а при билинейном преобразовании угол ф (co/Qo) = 2 arctg co/Qo возрастает нелинейно; при стремлении (О ± °° угол ф (co/Qo) стремится к своим предельным значениям ±я. Таким образом, вся ось tco/Qo р-плоскости трансформируется на г-плоскости в один обход окружности г= 1 и тем самым обеспечивается взаимнооднозначное отображение р на г для всей р-плоскости.

Сопоставление функций eVii/Qo) и е<" позволяет трактовать ф (co/Qo) = = 2 arctg co/Qp как эквивалентную частоту соТ (безразмерную), связанную с обычной частотой со, используемой при анализе и синтезе аналоговых цепей, соотношением

со„Т = 2 arctg (co/Qo). (15.74)

Соответственно

co/Qo = tg(co„ 7/2). (15.75)

Нормирующую частоту Qo можно определить, установив соотношение между какими-либо характерными частотами передаточных функций аналоговой и цифровой цепей. Например, если речь идет о цифровом ФНЧ с заданной частотой среза соц, эквивалентном (в смысле АЧХ) аналоговому фильтру с частотой среза со, то выражения (15.74), (15.75) можно записать так:

co,„r = 2arctg(co,,/Qo). со/о = tg (со., Г/2). (15.76)

Из последнего выражения следует, что o = «ca/tg(«c«7/2).

Пусть, например, частота среза цифрового фильтра должна составлять 10% от частоты дискретизации 1/Т. Тогда

Т-0,1.2я и tgK„T/2) = tg(0,1.2n/2)=tgl8° = 0,3249,

а выражение (15.74) переходит в

соц Т = 2 arctg [(tg соц Т/2) а/а)] = 2 arctg (0,3249д;), (15.77)

где X - (о/сОра - нормированная частота, использованная при аппроксимации АЧХ аналогового фильтра (см§ 15,5, 15.7).

Полученное соотношение между сОцТ и х позволяет построить АЧХ синтезируемого цифрового фильтра по заданной характеристике исходного аналогового фильтра. В качестве последней на рис. 15.19, а показана АЧХ фильтра Чебышева (при п = 2), рассчитанная в § 15.7:

\K{ix)\lVl+TUx}

АЧХ цифрового фильтра представлена на рис. 15.19, б. Видно, что эта характеристика, сохраняя масштаб на оси ординат, сжимается на оси абсцисс в пределах - я сОцТ < л.

Обратимся теперь к определению структуры и параметров синтезируемого цифрового фильтра.

Отталкиваясь от передаточной функции исходного аналогового фильтра [см. (15.42)1

К (Рх) = C/{Px~Pxni) (Рх -pIm), (15.78)

где Рх == (о -f to))/cuea - переменная, нормированная относительно частоты среза, и переходя к новой переменной р = (о + io))/Qo = 0,3249 рх, на основании выражения (15.72) получаем

р=0,3249р.= £, p.= ,j.

Подставим полученное выражение для рх в (15.78). Полюсы и pl„i, как и в примере, приведенном в § 15.7, равны соответственно -0,322 + + i 0,777 и - 0,322 - i 0,777.

После несложных преобразований приходим к следующему результату

1-fcjz-"

К (2) =

где \ = 2Re(2ni) и -i2„l\ 4-

- коэффициент нормирования.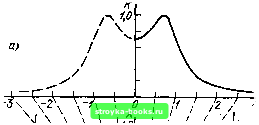

Рис. 15.19. Амплитудно-частотные характеристики аналогового (а) и соответствующего ему цифрового фильтра (б)

Н \ \ \ \ «-п

-3S0° -fW

\\\\у

/ /

ЪВО" й>иГ