Для определения постоянного коэффициента С подставим в последнее выражение S (п) из (12.14):

s(fe)=C 2 S s(/n)e «С у s{m) 2 e

2Л ,

При m = k внутренняя сумма обращается в Л, a при любом другом значении т в нуль (как сумма векторов, концы которых делят окружность единичного радиуса на равные дуги). Следовательно, в правой части остается одно слагаемое Cs (k) N, из чего вытекает равенство С = 1/Л. Таким образом, ОДПФ принимает следующую форму:

. 2я ,

s{k)-jj- У S(n)e , = 0, 1,..., Л/ -1. (12.15)

Вне интервала Ok N ~ \ ОДПФ определяет периодическое продолжение исходной последовательности s (k), показанное на рис. 12.7, в (левая часть).

Итак, дискретизованному сигналу {s {kT}}, А= 0,1, Л- 1, соответствует слугошнои спектр Sr («) с периодической структурой (рис. 12.7, б). Дискретизованному же спектру S (п.) соответствует периодическая последовательность сигналов {s (кТ)}, повторяемых с периодом Л (рис. 12.7, в).

Некоторые из свойств непрерывных преобразований Фурье, рассмотренных в § 2.8, нетрудно сформулировать также и для ДПФ.

1. Линейность преобразования. Спектр суммы (разности) дискретных сигналов равен сумме (разности) их спектров.

2. Сдвиг дискретного сигнала во времени. Повторяя рассуждения, приведшие к выражению (2.57), нетрудно показать, что если сигналу s (t).

представленному совокупностью отсчетов s (kT), к - 0,\..... Л - 1,

соответствует ДПФ S (лДсо), го сигналу s (t тТ), где т - целое число,

соответствует ДПФ е S (п Дсо). Иными словами, сдвиг последовательности отсчетов на т интервалов приводит лишь к изменению фазо-частотной

характеристики ДПФ на величину пт (теорема запаздывания).

3. Теоре.ма свертки. Если ДПФ S (пД со) соответствует дискретному сиг-

налу St (f) % S (кТ) 8 (t - кТ), а ДПФ G (пА<м) - сигналу gr (t) =

= 2l g (йТ)б (t - кТ), то произведению S (лАсо) G (лДо) соответствует сиг-

/г=0

нал (линейная свертка)

y(mT)=y\[(m--k}T]g(kT), N N,-hNg. (12.16)

При Л < jVj + Ng получается так называемая круговая свертка. Вывод выражения (12.16) аналогичен выводу (2.64) [см. также (12.3)1.

12.5. ПРИМЕНЕНИЕ МЕТОДА Z-ПРЕОБРАЗОВАНИЯ ДЛЯ АНАЛИЗА ДИСКРЕТНЫХ СИГНАЛОВ И ЦЕПЕЙ

При математическом описании дискретных последовательностей, а также дискретных цепей большую роль играет функция е". Изображения по Лапласу временных процессов, а также передаточные функции цепей, в в которые входит ер, оказываются трансцендентными функциями р, что существенно затрудняет анализ. Его можно упростить при переходе к новой переменной z, связанной с р соотношением

z - eP, л = -1пг.

(12.17)

При такой замене указанные функции от р преобразуются в рациональные функции от переменной г, благодаря чему упрощается представление их на плоскости г.

Преобразование плоскости = о + г« в плоскость z = х + г г/ можно осуществлять с помощью следующих соотношений, связывающих координаты Oj, cOj какой-либо точки р на плоскости р с координатами Xj, соответствующей точки Zj на плоскости z (рис. 12.9):

Zi=.Xi + J«/i = e« + ") A:i=e<cosWir, г/i = е" sin coi Т, • (12.18)

В полярных координатах на плоскости z

-i = Uil=K4+!-e<. 9i=.argZi = «i7 + m2K, (12.19)

где т - любое целое число.

На рис. 12.10 представлены отображения некоторых характерных точек и областей *-из /-плоскости на г-плоскость. Точка р = 0 переходит в точку г = 1 на вещественной оси z-плоскости. При движении точки /-плоскости вдоль оси ш (т. е. при 0 = 0) соответствующая ей точка г-плоскости описывает окружность единичного радиуса. Один полный оборот радиуса-вектора соответствует изменению частоты № в интервале coi ш cOj + 2л/Т.

При движении точки pi вдоль оси /со в пределах от - г оо до / оо точка Zi описывает бесконечно большое число окружностей. Таким образом, взаимно-однозначное отображение р яг Z существует только для

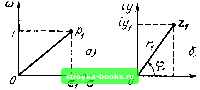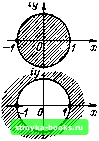Рис. 12.9. Соотношение между координатами точки на р-плоскости (а) и z-плоскости (б)

Рис. 12.10. Отображение точек и областей из р-плоскости иа г-плоскость

полосы р-плоскости между ± л/Т. Внутри этой полосы левая полуплоскость отображается внутрь единичного круга. Все параллельные полосы такой же ширины соответствуют этому же кругу. Правая полуплоскость р преобразуется во всю z-плоскость, исключая единичный круг.

12.6. z-ПРЕОБРАЗОВАНИЕ ВРЕМЕННЫХ ФУНКЦИЙ

Основываясь на приведенном в § 2.17 преобразования Лапласа дискретного сигнала [см. (2.125)1 и полагая е = z, получаем выражение

S(z) = Sr(p)

-L,.= Jo(>-* (12.20)

называемое прямым z-преобразованием (односторонним).

Комплексная функция S (z) определена только для области z, в которой степенной ряд (12.20) сходится.

Условие сходимости: s (/г) <С сг* при любых > О, где с> О - постоянное действительное число, а Го > О также действительное число, являющееся радиусом сходимости, зависящим от свойств последовательности {s (к)}, k оо. Поскольку (12.20) определяет ряд по отрицательным степеням z, область сходимости включает в себя всю z-плоскость, за исключением круга радиуса Гд, т. е. данный ряд сходится при Гд < z < оо.

В случае ограниченной последовательности {s {k)), * = 0,1.....N - 1,

в которой только конечное число членов отлично от нуля, для сходимости ряда требуется, чтобы z () <: оо, О - 1. При этом z может принимать все значения за исключением z = 0.

Найдем функцию S (z) и радиус сходимости для некоторых простых временных функций St (t).

1. Последовательность отсчетов из сигнала s(/) = 1, /0. В этом случае s (kT) = 1, fe == 0,1, 2, оо, и в соответствии с (12.20)

(z)= Vs(feT)z-* = ; z-* = --i-=.-. (12.21)

Нуль функции S (z) в точке Zo = О, полюс в точке z„ = 1. Радиус сходимости Го = 1; функция сходится при z > 1.

2. Последовательность отсчетов из сигнала s (/) = е~", / > О, В этом случае s (kT) = е""* и

*=0 А=0

1-е-"г-1

(12.22)

Нуль Zo = о, полюс Zn == е-«; Гд = е-«, z> е «- .

3. Последовательность отсчетов из сигнала s(/) = а", t.>0, a<il. В этом случае s (kT) = а«* и

5(г)= У а->Гг-=У(а-Гг-Г==-i-- =- (12.23)