продукты взаимодействия в НЭ сигнала с шумом, спектральный состав которых оказывается вне указанной полосы, могут не приниматься во внимание. Основной интерес в данном случае представляет вопрос о влиянии НЭ на соотношение между мощностью полезного сигнала и мощностью шума на выходе ограничителя в полосе частот, примыкающей к резонансной частоте СОц.

Для осуществления жесткого ограничения характеристике НЭ стараются придавать форму, близкую к представленной на рис. П.И (идеальное ограничение). В этом случае

i (и) =

а при U > О, О при U < 0.

(11.61)

При воздействии одного лишь гармонического сигнала ток приобретает форму меандра с амплитудой импульсов а. При этом амплитуда первой гармоники тока, воздействующей на нагрузочный контур, равна 2 о/я [см. (2.33)1 и мощность сигнала на выходе ограничителя пропорциональна величине Я, = 4i (2а/я) 2.

При воздействии одного лишь шума х (t) = А (t) cos [coq +6 (01 с нормальным законом распределения ток i (t) также имеет форму, близкую к меандру с амплитудой а, но со случайной длительностью импульсов т, флуктуирующей относительно среднего значения Хд = l/2/о, где fg - центральная частота спектра шума. Отличие тока от меандра заклюЧ"ается лишь в том, что моменты перехода через нуль являются случайными. Средняя-мощность при таком токе в резонансной нагрузке не отличается от приведенной выше величины / (2а/я) .

Таким образом, средняя мощность сигнала на выходе ограничителя не зависит от отношения сигнал-помеха на входе. При отсутствии полезного сигнала (Е = 0) вся мощность == l-i (2о/я) сосредоточена в узкополосном шуме. При отсутствии шума эта же мощность сосредоточена в сигнале, причем амплитуда Ад достигает в этом режиме максимально возможного значения Адах = 2а/п.

При одновременном воздействии s (t) их (t) амплитуда определяется выражением (см. [161) /

V2TI Ох

I £2 4ai

£2

(11.62)

где/i = £/2а, как и в выражении (11.36), есть отношение сигнал-помеха на входе устройства.

Составим отношение сигнал-помеха на выходе ограничителя. Основываясь на условии постоянства суммарной мощности = (2 о/л)*, получаем

AII2- лУ-е-[/о (ftV2) + /i (ftV2)p jjgg.

In /вых Р-А1/2 4 - " - - ----•

Учитывая, наконец, что - (С/П), приходим к следующему соотношению:

(С/П),

(С/П)в,. 4-я/.Че-/2 /„ (ftV2) + e-V2 (fta/2)f

(11.64)

34.5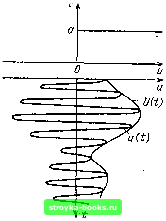

(С/П\

Bbix

Рнс. 11.12. Изменение соотношения между мощностью сигнала и мощностью шума в резонансном ограничителе

-Рис. 11.11. Жесткое ограничение узкополосного случайного процесса

График функции у {h) представлен на рис. 11.12.

При слабо.м в.ходном сигнале (Л < 1) функция г/ (h) л/4, а при сильном сигнале (h > 1) эта функция стремится к 2.

Отметим, что удвоение отношения сигнал-помеха при сильно.м сигнале совпадает с аналогичным эффектом подавления слабого колебания более сильным при ограничении суммы двух гармонических колебаний (см. § 8.7).

Из равенства у (Л) яь; л/4 (при < 1) вытекает, что в отличие от детектирования AM колебания (см. §11.5) в резонансном ограничителе практически отсутствует эффект подавления слабого сигнала сильной помехой.

Это свойство «идеального» ограничителя проявляется при симметричном распределении шума относительно нулевого значения (проведенное выше рассмотрение относится к нормальному закону).

11.8. КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ И СПЕКТР СЛУЧАЙНОГО ПРОЦЕССА В ЛИНЕЙНОЙ ПАРАМЕТРИЧЕСКОЙ ЦЕПИ

Пусть передаточная функция линейной параметрической цепи является вещественной функцией времени и не зависит от частоты. В § 10.2 было показано, что подобная передаточная функция характеризует цепь, в которой имеет место AM.

Обозначим передаточную функцию через К (t) (аргумент /со опущен), причем функция К (/) может представлять собой как детер.минированный, так и случайный процесс. Входной сигнал s (/) также может быть либо детерминированным, либо случайным процессом (с нулевым средним).

Составим выражение для ковариационной функции выходного сигнала 5вых (О

«вых ) = fBHX (/) «вых (/ + Т)1 = /И {К (/) K{t + T}S (t) S (t + T)J.

(11.65)

Нас интересует случай, когда передаточная функция К (/) не зависит от входного сигнала s (/). Тогда среднее значение произведения в (11.65) равно произведению средних значений соответствующих сомножителей, т.е.

вых ) ==- t/C (О K(t + т)] М is (О S (/ + т)Кк . т) /?, (/, г),

(11.66)

где Rs (t, т) - корреляционная функция входного сигнала, а

Кк {t, т) = М 1/С (О К((+г)\ (11.67)

- ковариационная функция цепи с коэффициентом передачи К (О-

Из выражения (11.66) вытекает важное свойство линейной цепи с переменными параметрами: корреляционная функция выходного сигнала равна произведению корреляционных функций входного сигнала Rs (t, т) и цепи Кк (t, т).

Для нестационарных процессов корреляционные функции в (11.66). (11.67) зависят не только от временного сдвига, но и от времени t. Этими характеристиками не всегда удобно пользоваться. Далее в примерах используются функции R (т), получаемые усреднением R (t, т) по t [см. (4.89)1.

Применяя преобразование Фурье к усредненной по времени функции вых (т). получаем также усредненный спектр выходного сигнала

вых(«)= ] /?вь,х (т) е---dT. (11.68)

- оо

проиллюстрируем использование соотношений (11.65)-(11.68) на примерах.

1. Гармонический сигнал s (/) = cos Wq Действует на входе линейной цепи с передаточной функцией

К (t) = Ко + (t). (11.69)

где Ко - среднее значение коэффициента усиления цепи; Д/С (О - флуктуация коэффициента усиления, представляющая собой нормально распределенный стационарный случайный процесс с дисперсией ак-

Для полной характеристики изменения во времени передаточной функции цепи должны быть заданы либо ковариационная функция Kj (т), либо спектр Wj (ы) случайного процесса К (О-

Очевидно, что постоянной составляющей Ко соответствует спектр Кко (ы) = === 2яАГоб (ш). Спектр второго слагаемого, т. е. А/С U), зададим в форме

(й,)=г2с/(я2+о.П.

где а и с - постоянные величины.

Таким образом, спектр суммы /Со + (t)

Г(ш)=2л/<Н«(й)) !-2c/(fl2-*-,o2). (11.70)

Заданному спектру 117д. (ы) соответствует ковариионная функция

оо оо

Кк (т) = f (Q) е" do. = J 2яК§ б (ш) е"« +

- СО - оо

+ Т- f -т!4"" = § + -е-"- (И.71)

2я J а + (л а

- оо

Найдем корреляционную функцию и спектр мощности сигнала на выходе цепи. Имея в виду соотношения (11.66) и (11.71), а также учитывая, что корреляционная функция сигнала s (t) - cos (Hq} равна

Rs (t)=-/2COSWoT,

Действительно, для постоянной составляющей Ко корреляционная функция равна /С§. Следовательно, по формуле (11.68) энергетический спектр

Wo (ft.) =/(2 J e-** dx=2Kj б (О)) \

- со