
 |
|
Главная Нелинейные системы управления [ 0 ] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] Нелинейные системы управления К нелинейным системам относят все системы, которые не могут быть описаны линейными дифференциальными уравнениями. Множество нелинейных систем настолько широко и многообразно, что практически нельзя говорить о едином «классе» нелинейных систем, противостоящем классу линейных систем. В данной главе рассмотрен значительно более узкий, хотя и широко распространенный в практике управления, класс нелинейных систем, характеризуемый следуюш,ими особенностями: систему можно представить в виде соединения двух частей (рис. 7.1) - линейной части ЛЧ, описываемой линейными обыкновенными дифференциальными уравнениями с постоянными коэффициентами, и нелинейного элемента НЭ. Нелинейный элемент является безынерционным, и его входная X и выходная у величины связаны между собой нелинейными алгебраическими уравнениями. Таким образом, нелинейность рассматриваемых систем обусловлена нелинейностью статической характеристики одного из ее элементов. Если система содержит несколько нелинейных элементов, то ее в некоторых случаях можно свести к рас<;матри-ваемому классу, заменив нелинейные элементы одним с результирующей ста- 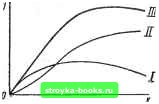 Рис. 7.1 Рис. 7.2
тической характеристикой. Например, при параллельном, последовательном или встречно-параллельном соединении нелинейных элементов такое сведение выполнимо. На рис. 7.2 приведен пример нахождения результирующей статической характеристики двух параллельно включенных нелинейных звеньев. Построив на одном графике характеристики il и обоих звеньев, суммируем их ординаты и получаем характеристику / эквивалентного звена. На рис. 7.3 показано нахождение результирующей характеристики двух последовательно включенных нелинейных звеньев. В первом квадранте построена статическая характеристика / входного звена цепочки, во втором квадранте - характеристика следующего звена, но так, что оси ее повернуты на 90°: ось абсцисс Лгвх совпадает с осью ординат характеристики /, а ось ординат Хгвых направлена по отрицательной полуоси абсцисс. Задаемся некоторым значением л;, (точка /вых на -"iBx)- Восставляем перпендикуляр в точке / до пересечения с характеристикой / (точка 2); проводим из точки 2линию, параллельную горизонтальной оси, до пересечения с характеристикой (точка 3). Отрезок Оа от на- 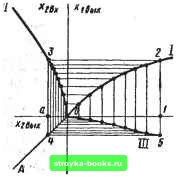 Рис. 7.3 чала координат до основания перпендикуляра, опущенного из точки 3 на ось абсцисс, равен искомому значению Xjux. соответствующему XiBx- Неудобнее построить характеристику / в четвертом квадранте, поэтому перенесем точку 3 с помощью биссектрисы OA квадрантного угла, проведя из точки 3 вертикальную линию 3-4 до пересечения с OA (точка 4) и из точки 4 горизонтальную линию 4 - 5 до встречи с продолжением перпендикуляра /-2 (точка 5). Точка 5 принадлежит статической характеристике / эквивалентного звена. Находя аналогичным способом ряд точек и соединяя их плавной кривой, получаем результирующую характеристику /. Наиболее просто строится характеристика последовательного соединения трех звеньев. Характеристики I и II располагаются, как и в предыдущем случае, в первом и втором квадрантах, характеристика / третьего звена - в третьем квадранте вместо биссектрисы с соответствующим поворотом осей (рис. 7.4). На рис. 7.5 построена результирующая характеристика / нелинейного звена /, охваченного нелинейной отрицательной обратной связью с характеристикой (рис. 7.5, а). В первом квадранте (рис. 7.5, б) построена характеристика звена /. Задаемся некоторым значением лых (точка /) и найдем, чему будет равно лх при наличии обратной связи. Без обратной
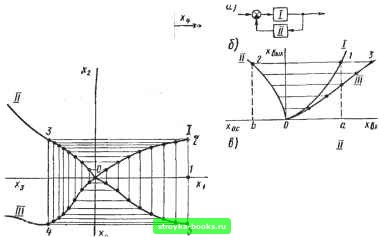
Рис. 7.4 Рис. 7.5 [ 0 ] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |