Например, обе строки 1 и 2 в (7.1) содержат единицы в столбцах 3 и 5; поэтому множество (1, 2) первого перечня заменяется множествами (1, 2, 3} и {1, 2, 5}. Так как в матрице нет столбцов, в которых обе строки 2 и 4 содержат единицу, то множество {2, 4} из первого перечня заменяется множеством {2, 4}. Из (7.1) и второго перечня можно найти третий перечень: {1, 2, 3, 5}, (2, 4], (3, 6}, {4, 6}. Так как этот перечень такой же, как и четвертый, то он содержит все С-множества автомата Л32.

Минимальная форма Л32, а именно Л32 соответствует наименьшей правильной группировке, построенной из перечисленных С-множеств или из подмножеств этих С-множеств. Так как каждая группировка должна содержать все шесть состояний, минимальная правильная группировка должна иметь мощность 2 или больше. Однако, так как группировка (1, 2, 3, 5}, {4, 6} не является правильной, нижняя граница мощности, равная 2, недостижима. При помощи таблицы 7.2 можно легко проверить, что {1. 2], {3, 5}, {4, 6} составляют правильную группировку; поэтому эта группировка и есть минимальная правильная группировка. Можно легко проверить, что {1, 5}, (2, 4} и {3, 6} составляют другую минимальную правильную группировку. Отсюда следует, что минимальная правильная группировка автомата с ограничениями на входе не всегда однозначна. Значит, заданный автомат с ограничениями на входе может иметь несколько минимальных форм, которые не обязательно изоморфны друг другу.

Как только получена минимальная правильная группировка автомата М, может быть получена таблица переходов соответствующей минимальной формы М из таблицы переходов М следующим образом.

Алгоритм 7.2. Дана минимальная правильная группировка автомата М, а именно Sj, Sj, .... S„, где есть

Oi , Oi.....Oi 1; надо построить минимальную форму М

12 r.J

с множеством состояний а[, о.....о}. (1) Полагаем k=l.

(2) (а) Если все клетки в подтаблицах- и s. автомата М, расположенные на пересечении строк 0*, о*.....о* и

столбца Ij, содержат прочерк, то в Клетках подтаблиц z

И s+i автомата Ж, расположенных на пересечении строки и столбца Ij, тоже проставим прочерк, (б) Если, по крайней мере, одна из клеток в подтаблице автомата М,

расположенных на пересечении строк Oj , Oj.....о* и

ft

столбца Ij, не содержит прочерка, то проставим содержимое

таких клеток в клетке, расположенной на пересечении строки о

и столбца Ij в подтаблице z автомата М. (в) Если в подтаблице s.] автомата М есть клетки без прочерка, располо-

женные на пересечении строк о*, 0*

Oji и столбца Ij,

то находим совместимое множество 2, в которое включены все элементы, соответствующие этим клеткам. Пусть о будет содержимым клетки, общей для строки и столбца у

в подтаблице s+j автомата М. (3) (а) Если ft < л, то увеличиваем ft на 1 и возвращаемся к (2). (б) Если k = n, то

таблица переходов для М построена.

Таблица 7.3 представляет собой таблицу переходов автомата Л321, который является минимальной формой автомата Л32.

Таблица 7.3 Автомат i432i

Таблица 7.4 Автомат Л322

Эта таблица построена на основе минимальной правильной группировки (1, 2 , (3, 5}, (4, 6}. Множества группировки представлены в Л32) состояниями 1, 2, 3 соответственно. Таблица 7.4 представляет собой таблицу переходов автомата Л322. являющегося минимальной формой Л32. Таблица построена на основе минимальной правильной группировки

f.S\

МЕТОД УМЕНЬШЕНИЯ ЧИСЛА СбСТОЯНИЙ

{1,5}, {2,4}, {3,6}, множества которой представлены в л322 состояниями 1, 2, 3 соответственно.

На рис. 7.2 и 7.3 приведены графы переходов автоматов л321 и л322 соответственно. Для иллюстрации квазиэквивалентности автоматов л32), л 322 по отношению к автомату л 32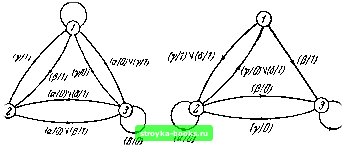

Рис. 7.2. Автомат A32i.

(amip/nw/fj

Рис. 7.3. Автомат 32,.

рассмотрим входную последовательность yy«Y«PY«YPP> которая допустима для состояния 1 автомата л32. Когда эта последовательность прикладывается к л32 в состоянии 1 или к Л321 в состоянии 1, или к л322 в состоянии 1 (два последних состояния квазиэквивалентны первому), видно, что реакция автоматов на эту последовательность одинакова у всех автоматов и выражается так: 10101100000111.

7.5. Метод уменьшения числа состояний автоматов с ограничениями на входе

Как стало ясно из предыдущих параграфов, определение минимальной формы автомата с ограничениями на входе - процесс очень трудоемкий. В тех случаях, когда не обязательно требуется минимальная форма, но уменьшение числа состояний все же желательно, может быть использован упрощенный метод, который часто дает значительно сокращенную форму (а иногда и минимальную форму) по сравнению с заданным автоматом. Предлагаемый метод, по существу, является методом таблиц Р минимизации автоматов без ограничений на входе, описанным в § 3.6. Единственное различив