
 |
|
Главная Развитие народного хозяйства [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [ 83 ] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] Идентификация Тип, уравнение и передаточная функция динамического звена (регулятора) Переходная функция fc(0 Схема модели Безынерционное звено (П-регулятор) вых = fe-Bx; Я(р) = й h(i} Идеальное интегрирующее звено (И-регулятор) <!Х, ОоР Р сел t Инерционное звено (апериодический регулятор) + -вых = feXBx; h(i) Изодромное звено (ПИ - регулятор) = Хвх + Щр) = ОоР «о Колебательное звено вых , «о -7Г,--Ь +«1 + Хвых = = кАвх; Я(р) = k с„р= -f- СР -1- 1 .  а линейных звеньев САР
(,ВЫХ1 - -ВХ - «1 (,- 1).БЫХ1~ - Х(/-1),вых1; А Хь, = X ; ,3, X Ebixl=(t l),Bbixl+t,Bbixi; А XiBuxi = i.nuxl XjBbixi - = X(t-1),Вых1 + А Xj- Bbixi; XiBblx = - Xj Bbixi SUBROUTINE КОЛЗ (XI, X2, X3, DT, A, AI, K, X22, X21, DIX, DOX) X22=X1-AI* X21-X3 D1X=X22 * DT/A X21=X21+D1X D0X=X21 * DT XS=X3--D0X X2=X3 * К RETURJN END CALL КОЛЗ (XI, X2, X3, DT, A, AI, K, X22, X21, DIX, DOX) Тип, уравнение и передаточная функция динамического звена (регулятора) Переходная функция h{t) Схема модели Консервативное звено вых , + -вых = = feBx; Интегрирующее звено с замедлением й«-т:;--г = ЙХвх; Я(р) = p(l-f-floP) 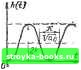
1 вь,х1  ч,еык1, а Инерционные звенья высших порядков • • • "Ь .вых = Н{р) = k Xpn-i+...-\-l ------ [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [ 83 ] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] 0.0013 |