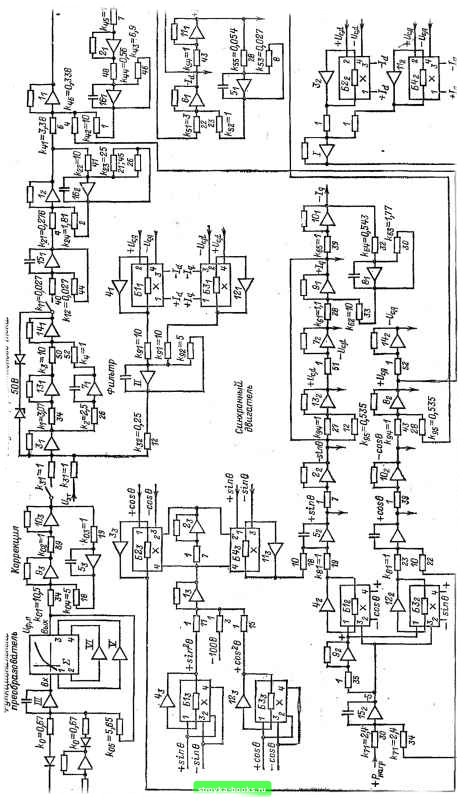1Я со

Постоянная времени демпферной обмотки при замкнутых обмотке статора и обмотке возбуждения =0,008 с.

Постоянная времени демпферной обмотки при разомкнутых обмотке статора и обмотке возбуждения 70=0,0565 с.

Постоянная времени обмотки возбуждения при замкнутой обмотке статора и

разомкнутой демпферной обмотке =

= 1,23 с.

Постоянная вермени регулятора реактивного тока 7р,р,т=0,04 с.

Постоянная времени положительной обратной связи по активному току Га,р = =0,05 с.

Постоянная времени фильтров измерителей Гф=0,02 с.

Постоянная времени обмотки возбуждения при разомкнутой обмотке статора

Tdfi =3,7 с.

Решение. В соответствии со структурной схемой рис. 1-309 и табл. 1-43 схема набора на моделирующей установке принимает вид, показанный на рис. 1-310. Выбор масштабов и определение коэффициентов усиления звеньев на модели

а) Регулятор тока возбуждения

Регулятор реактивного тока

Принимаем масштаб эталонного напряжения и масштаб выходного напряжения регулятора соответственно mj =

=/«„ = 10.

Тогда регулятора

Р.р.т

1,23-10 0,04-10

= 30,75;

для интегральной части регулятора

0,04-10

= 25.

Р,Р,т "и

Функциональный преобразователь Принимаем масштабы активной и активной мощности

mp=mQ = 20.

Масштаб входного напряжения преобразователя niypo =10.

Масштаб выходного напряжения преобразователя т,, =2,84.

Масштаб выходного напряжения ин-

тегратора Шц =8. Тогда

"(Уин

0,05-10

1/Ро

-1/Ро = 16;

2.84

= 3,52;

[ро) Ро

1,19-20

= 0,42.

Расчетная зависимость между входным и выходным напряжением функционального

Коррекция

Р =Р -

= 1,19-- = 4,2.

2,84

б) Синхронный двигатель

Принимаем масштаб переменной на выходе звена Н{р)

тд = 10;

масштабы токов

т - mj = nij =20;

масштабы напряжений

led

= гпл = 100.

для пропорциональной части тогда

Xa.f,d\ Xa.f.a С

= 1:

Ха niQ 1,073-10

736 100 100

= 1,86;

/ 1 \ 1 "1/ 1 20

I-1 =---- =-• -= О 272-

[Xj ~ Хд mj 0.736 100 •

= 0,107

= 0,535.

Обратная связь по Uc.q

= fe,

о,си.

c,q т

= 1-0,1.

Принимаем масштаб скольжения ms= =3140, масштабы для sin 6 и cos 6: msin= =mcos = 100. Тогда

Ш„ = СОг

р

= 314-

1-3140 6,55-20 100

= 24;

3140

= 10.

Совмещаем фильтр и сумматор реактивной мощности

тф = тэт; fQ

00-20 -9П

Определение коэффициентов усилення на входах операционных усилителей

а) Регулятор тока возбуждения

Регулятор реактивного тока kiks=l/„p=30,7. Принимает fei = 3,07; k = = 10;

к„ 25

k2ki=- = - =2,5. Принимаем k =2,5;

mt 10 ki=l; масштаб времени mt = 10.

Функциональный преобразователь

1 Y *нн 16

- = 0.42--=0,67; mt 10

5,65.

Коррекция

feo2feo3V-y, 10.0,02

Принимаем о2=оз=1; йо4=5. Фильтр

= 5.

32 91 - 31 *92 =

10-0,02 1

-2.5;

==5.

mt Тф 10-0,02 Принимаем 2=0,25; 91= 10. в) Синхронный двигатель Звено Н(р)

\ rf j

0,004 0,0145

= 0,276;

nitlk4 10-0,004 1

22 24 = 23

= 25;

t d.o

= 25-

-= 18,1.

10-0,0145 Принимаем 22= 10; 24=1,81;

fen = fei2 =--:- = "

d,o

10-3,7

= 0,027.

Звено J/Xd(p)

1 ут.

I 1 \Td.Q 0,0145

= 6,9;

ki2 fe44 fe45 = 1

10-0,0145 1

- 6,9 = 5,6,

10-0,008

Принимаем fe42=10; fe44=0,56; 45==!;

fe.« = -

10-3,7

= 0,027;

fe52 few fees =•

-~fe53 =

- 0,027 = 0.054.

10-1.23

Принимаем fe52=fe54=l; fe55=0,054. Звено l/Xg(p)

-Hi)

fens ==

T.o 0,0565

- = 0,272--

T 0,0139

"t ЧО feea fe64 feefi = 1

10-0.0565 1

= 1.1;

1.77;

fees =

1.77 = 5,43.

10-0,0139

Принимаем fee2=10; fe64=0,543; fee5=l. Звено скольжения s и угла 6

fe,i =

kgi = -

пц mt

24 10

= 2,4;

10 10

= 1.

В данном примере для набора на модели звено Н (р) структурной схемы синхронного двигателя разбивается на два звена: интегрально-дифференцирующее и апериодическое, а звено 1/Ха{р)-на два иитегрально-дифференцирующих звена.

Масштабы напрялсений Uc,d и Uc,q, а также величина sin 0 и cos 6 выбраны равными 100 нз условия обеспечения мини-