fт = Фи - arctg

(1-344)

<lio=arctg

- arctg

. (1-345)

На рис. 1-291-1-296 приведены полученные с помощью цифровых ЭВМ номограммы основных показателей переходных процессов в системе 2-1-2, охватывающие апериодический и колебательный режимы.

К этим показателям относятся:

1) первый (положительный) максимум

при импульсном воздействии /и, max,

2) обобщенное время первого согласования прн ступенчатом вооздействии сОс ti (соответствует максимуму скоростной ошибки);

3) обобщенное время достижения первого максимума при ступенчатом воздействии Ис и, шах-,

4) максимум единичной переходной функции при ступенчатом воздействии

/т max,

5) обобщенное время отработки ступенчатого воздействия «с от начала процесса до времени, когда значение /т(0 отличается от установившегося значения не более чем иа 5%;

6) максимум скоростной ошибки fo. max-

На рис. 1-297 приведены единичные переходные функции системы 2-1-2 для т = = 2 и я = 1/2, соответствующие симметричному оптимуму.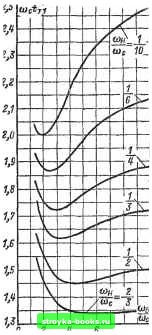

8 10

Рис. 1-291. Обобщенное время первого согласования единичной переходной функции при ступенчатом воздействии.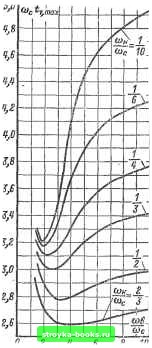

Рнс. 1-292. Обобшеппое время достижения первого максимума прн ступенчатом воздействии.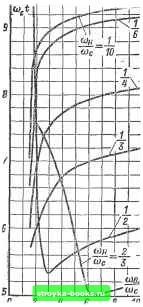

Рис. 1-293. Обобщенное время отработки ступенчатого воздействия.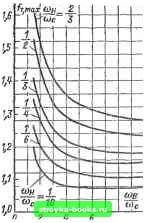

8 10

Рис. 1-294. Максимум единичной переходной функции при ступенчатом воздействии.

0,S« 0,90 D,8B D,8Z D,78 0,71 0,70

Djse

C.6Z

Рис. 1-295. Максимум единичной переход-вой функции при импульсном воздействии.

Основные показатели при этом равны: =2 = 0,825; «е т. шах = 2,9; Шс ty = = 7,2; сос <т1 = 1,4; f-r.max = 1ЛА;

«с /о.ша»: = 0,88.

Задержанная обратная связь. Наряду с системами регулирования с неизменно!": струюгурой в настоящее время нашли широкое использование системы с переменной структурой, в общем случае обеспечивающие более высокое качество регулирования. В некоторых слу«!аях перемена структуры определяется изменением режима работы ксполнительных органов системы регулирования. Так, например, в регулируемом вентильном электроприводе постоянного тока при переходе от ггепрерывного режима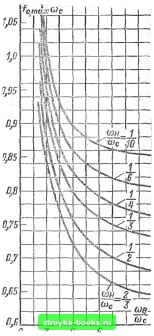

8 10

Рис. 1-296. Максимум скоростной ошибки.

проводимости тока к прерывистому видоизменяется структура звена преобразователь-электродвигатель. При этом компенсация указанных . изменений может быть произведена соответствующей коррекцией структуры регуляторов. В общем случае с точки зрения динамических свойств замкнутых систем регулирования перемена структуры эквивалентна режиму работы регуляторов с ненулевыми начальными условиями. Этот релшм, как будет показано ниже, характерен наличием в системе, кроме основных управляющих и возмущающих воздействий, дополнительных возмущающих воздействий, которые оказывают сущест-пенное влияние на характер переходных процессов и в то же время не влияют на установившиеся значения регулируемых параметров.

Одной из разновидностей систем с переменной стр5Ч{турой являются системы с задержанной обратной связью, т. е. такие системы, которые замыкаются не с момента подачи управляющего или возмущающего воздействия, а при выполнении определенных условий.

Системы с задержанной обратной связью составляют такой класс нелинейных систем, в которых нелинейность проявляется в скачкообразном переходе от одной линейной структуры к другой. Эта особенность указанных систем позволяет применить к ним известные методы структурных преобразований линейных систем (рис. 1-298) и сформулировать следующую мето-

дику определения реакции У этих систем на внешнее воздействие X.

В месте замыкания системы определяется возмущающее воздействие Х\, заменяющее все фактические задающие и возмущающие воздействия. Воздействие Xi прикладывается к видоизмененной замкнутой системе (рис. 1-289,6), в которой прямые звенья расположены от места замыка-

чины, определяемых ненулевыми начальными условиями. При этом все фактические управляющие и возмущающие воздействия иа систему сохраняются, но к ним добавляются воздействия, определяемые ненулевыми начальными условиями системы.

Ниже приводятся примеры использования указанных способов для определения динамических свойств некоторых достаточ-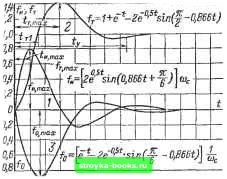

Рис. 1-297. Единичные переходные функции системы 2-1-2 для симметричного оптимума.

2е с sin X

1 - реакция иа импульс = X Jo.866a t--""с

ступенчатое воздействие fj, = 1 -- е "с -j. -f 2е~" """с * sin0,866cDg t-- 3 - асоростная

; 2 -реакция на - со„ i

ошибка =

,-«>с 2.-°-«сшХ

,866со„ i-f

Рис. 1-298. Структурная схема системы с задержанной обратной связью.

а -исходная структурная схема; б - преобразованная структурная схема.

ния системы до выходного сигнала, а результирующая обратная связь образована остальными прямыми звеньями вместе со звеньями обратной связи исходной системы.

Для определения реакции систем с задержанной обратной связью в некоторых случаях целесообразно использовать принцип суперпозиции для непосредственного выделения составляющих выходной вели-

VD1 VUZ

i-fccj-а-.

Eg. п

и. Л.

Рис. 1-299. Схема задатчнка интенсивности.

а - исходная функциональная схема; б - преобразованная структурная схема ; в - статическая характеристика компаратора.

но распространенных в электроприводе систем регулирования.

Примером системы с задержанной обратной связью является задатчик интенсивности (ЗИ), содержащий компаратор /, интегратор 2 и инвертор 3 (рис. 1-299). При подаче на вход компаратора ступенчатого управляюш,его сигнала Ез и нулевых начальных условиях на интеграторе нарастание выходной величины интегратора Е будет происходить по линейному закону до тех пор, пока она не достигнет значения Ее, при котором начинает проявляться действие обратной связи ЗИ, так как результирующий входной сигнал компаратора входит в линейную зону его статической характеристики.

Преобразованная в соответствии с изложенной методикой структурная схема этой системы представлена на рис. 1-299,6-

Ее реакция до момента замыкания определяется выражением

v:=v. (..з4<,

в момент замыкания системы Ез /гзам

г/в = £о =

(1-347)

где 7 = гзС - постоянная времени интегратора 2; k - коэффициент усиления компаратора /.