Таблица 1-36

Переходные функции системы 1-2 апериодического режима

Реакция

Изображение

Оригинал

На импульс

(р + «i) (р + щ)

f = mal i-i-

Ha ступенчатое воздействие

p (p + «1) (p -f ш-г)

£1)1 -«2

Скоростная ошибка

fo=-

p-f mcoc

p (p + «1) (p -f «2)

j/m? - 4m.

Моменты времени наступления максимума можно определить из следующего выражения:

«о и,77

X 1п

V т?-4т

I + Ут - 4т -Km? -

(1-311)

На рис. 1-284 представлены кривые =f{m) и fs,max=f(m). Их анализ

Ш 1

2,Б 3,2 2,8 2,4 2,0 1,6

-0,9 -0,8 -0,7 -0,6 -0,5 -ОН

0 2 4 6 8 10 12 14 IB i8

Рис. 1-284. Кривые (i)otn,max=f{m) и fli,max=f(.m) для СИСТСМЫ 1-2,

показывает, что при изменении /и от 4 до 20 значение ч>в1ж,тах изменяется в значительно меньших пределах (от 2 до 3,22); fu.max также изменяется в небольших пределах (от 0,735о)с до 0,89£йс).

Для определения и.таж справедливо следующее приближенное равенство;

(1-312)

Время переходного процесса для реакции на ступенчатое воздействие приближенно определяется из выралеения ?у,т = = 3/ш2, так как другая экспоненциальная составляющая затухает значительно скорее.

Колебательный режим (табл. 1-37). Для колебательного режима (т<4) передаточная функция замкнутой системы 1 -2 имеет следующий вид:

Язам (Р) =

(p+a)?-f р?

, (1-313)

Реакция на импульс достигает максимального значения при 1н,тах = (р/Р.

При малых значениях ф, когда т-4,

humax = -Г- = - • (1-315;

Р «о

Кривые (uotn.max = f{n) И fti,maxf(m)

на рис. 1-284 охватывают как апериодический, так и колебательный режимы.

Перерегулирование при ступегиатом воздействии

зга

От,гу.оз: = т,тах-1=е - (-316)

Время достижения первого максимума при ступенчатом воздействии

Ti.max

(1-317)

Таблица 1-37

Переходные функции системы 1-2 колебательного режима

Реакция

Изображение

Оригинал

На импульс

(рН-а)? + р2

На ступенчатое воздействие

sm (

. sm (р/ -Ь Ф)

Ф = arctg

Скоростная ошибка

p[(p-f а)Н-Р]

o = -

«с

.sin(

-sin (P/-f Ф)

Время достижения первого установившегося значения

П- ф

0-318)

Перерегулирование скоростной ошибки

.1 8Шфв~°1 о.тах - / ojnax - п

«с Р

(1-319)

Время наступления Со,тах равно ti. Система 1-2, у которой т=2, обычно называется системой, настроенной на техниче-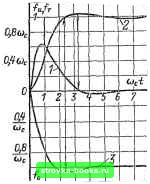

Рис. 1-285. Единичные переходные функции системы 1-2 для пг=2,

/ - реакция на импульс = 2е "с sin f-г -реакция на ступенчатое воздействие ~ ~ -- У2е~ ""с * sin cDp t + --j ; , 3 - скоростная

ошибка fr,= ---. - e "с *sin fcD„ i-j--

ский оптимум. Ее переходные функции приведены на рис. 1-285.

Для этой системы а=Р=(йс; Ф=л/4;

1,57 0,785 «и,тазс= = > /и.тазс-J.Do<ac;

«о «с

2,35

tT.max = 0,0435, /т1,тазс = ; j

(Ос (Ос

Оо,таж = 0,067.

Пример определения основных показателей переходных процессов для системы, изображенной на рис. 1-283.

Задание на путь изменяется по линейному закону с постоянной скоростью 0,2Йц. Требуется найти законы изменения пути; проходимого приводом при т=2, (Ос =

= 1 1/с, Гэм=0,1 с, /н/?/£д,а = 0,05, /<,т = 0.

Закон изменения пути Q=f(t) может быть найден с помощью уравнения для скоростной ошибки (см. табл. 1-37).

Динамическое рассогласование меж,ау заданным и действительным положениями следящего привода

де = 63-6(0 = 0,2 Йн/о (О == e-°sin(p/-f Ф)

0,2 Й„

= 0,2Й„

sin ф е-* sin (/ +

0,707

Ф = Гь/4; (Х=р = (Ос= 1 1/с.

Система 2-1. ЛАЧХ системы 2-1, являющейся астатической системой регулирования с астатизмом 2-го порядка, приведена на рис. 1-286.

Эта система образуется при последовательном соединеши интегрально-пропорционального звена с интегральным звеном. Системе 2-1 свойственна нулевая устано-

28 24 20 1В 12 8 Ч D

Рис. 1-286. Логарифмическая амплитудно-частотная характеристика системы 2-1.

вившаяся скоростная ошибка. Ее передаточная функция в разомкнутом состоянии

Яр (р) =

Частота среза

рТш1 рТж«

«с =

Язам(р) =

Тш1 Тиг tOo Ти! Тиг ai

tOc (р + tOp)

(1-320) (1-321)

Передаточная функция замкнутой системы 2-1

p?-f р«с + «о «с

(1-322)

Характер переходных процессов зависит от значения т=й)о/£йс. При т < - имеет место апериодический режим, при т > --колебательный. Значение т=1/4 соответствует критическому режиму, гра-

ничному между апериодическим (табл. 1-38) и колебательным.

При т < -уравнение (1-322) преоб-

разуется

Язам (Р) =

Шс (Р + т(йс) (P+«i) (Р + «2)

(1-323)

(1-324) (1-325)

Для системы 2-1 реакция на импульс fn при /=0 имеет значение, равное «с независимо от значения т.

При отработке ступенчатого воздействия системе 2-1 свойственно перерегулирование, обеспечивающее уменьшение скоростной ошибки до нулевого значения.

На рис. 1-287 изображены единичные переходные функции для /и =1/6.

Время наступления максимума /т

1 + К 1-4т l-Vl-4m V 1-4m

(Ь326)

©с

Время первого согласования fi (первого достижения значения fi.y)

1,max

(1-327)

Ему соответствует максимум скоростной ошибки

f о.тах -

е 2 -е

Oil -Mg

(1-328)

Таблица 1-38

Переходные функции системы 2-1 апериодического режима

Реакция

Изображение

Оригинал

На импульс

Шс (Р + тСс) (Р + «i) (Р + «2)

[(ш1-Шо)е-«*-

6Н - Щ -(ш2-Шо)е-"*]

На ступенчатое воздействие

<£>с (Р + "Юс) р (р -f Ш1) (р -f Ш2)

/т=1-

Шс (Mf - Шо) со. t (Ш1 -Ш2)

Ос («2 - tOo) а, t Шз (Ш1 - Шг)

(Р + Wi) (р + Шз)

fo =

p~<i>2t g- со, i Mg- Ml