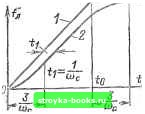Рис. 1-279. Линейное изменение задания и выходной величины в системе 1.

/ - изменение задания; 2-изменение выходной величины.

реакция на ступенчатое воздействие

-Q„ t

/т=1 скоростная ошибка 1

(1-296)

(1-297)

Соответствующие кривые представлены на рис. 1-278, где по оси абсцисс отло}кен безразмерный временной параметр Ис/. Под продолжительностью переходного процесса понимается время от начала процесса до того момента, когда значения функций отличаются от своих установившихся значений не более чем на 5%.

Для систем 1 это время определяется по выражению

Мс/у = 3. (1-298)

На рис. 1-279 изображено линейно-нарастающее задание, достигающее установившегося значения при t=to, и изменение выходного значения. Из рнс. 1-279 следует, что в начале процесса скоростная ошибка равна нулю, а через время /у«3/мс она достигает 95% своего установившегося значения, равного 1/Ис. После этого выходная величина нарастает практически с той же скоростью, что и задание, отставая от него во времени на /i=l/(Sc.

С момента прекращения роста задания (to) для выходной величины понадобится время /у!«3/(0с, прежде чем она достигнет практически установившегося значения.

Система 1, являясь астатической системой первого порядка, имеет установившуюся скоростную ошибку, равную 1/Wc-

Система 0-1 (ЛАЧХ на рнс. 1-280, кривая /) представляет собой апериодическое звено с коэффициентом усиления к и постоянной времени Т. Частота сопряжения участков с нулевым и единичным наклоном (00=1/7-.

При единичном ступенчатом воздействии установившаяся ошибка системы 0-1 равна:

А = . . , или при ft > 1 Д »-.

1-f ft

Ее передаточные функции в разомкнутом и замкнутом состоянии соответственно равны:

1 + рГ р -f (

Wo

(1-300)

Язам (Р) =

k<i>o

(1-301)

p + (ft-f 1)(0о

Установившаяся ошибка для системы 0-1 не равна нулю и определяется уравнением (1-299).

Ошибка системы 0-1 при линейном возрастании задания имеет две составляющие: одну тождественную скоростной ошибке в системе 1, и вторую, возрастающую линейно из-за конечной статической ошибки по заданию (рис. 1-281). Вторая составляющая называется позиционной ошибкой.

При ft>l (практически при ft>5) частота среза (Oc«ft(0o (ошибка менее 4%) и оригиналы функций (табл. 1-35) принимают вид:

1 + ft

/и = (Осе / k+i

(1-302)

(1-303)

1+ft (Ос

1 -е

(1-304)

Несмотря на то что в установившемся режиме система 0-1 имеет принципиальные отличия от системы 1, в переходных режимах (за период от О до Зозс/) для значений ft>5 обе эти системы ведут себя практически одинаково.

20 16 12 8 Ч О

ьс 0,8uc О.Выс 0,Чь>с 0.2ы, О

2 woi * 5 6 У 8910 ыО

05 1

(1-299)

Рис. 1-280. Логарифмическая амплитудно-частотная характеристика и единичные переходные функции системы 0-1 для

/ - ЛАЧХ системы; г-реакдия иа импульс; 3 - реакция на единичное ступенчатое воздействие.

Рис. 1-281. Ошибка системы 0-1 при линейном возрастании задания для ft=5.

/ - позиционная ошибка: 2 - скоростная ошибка; 3 - результирцощая ошибка.

20 16 12 8 4

20lg%(j<j)\

fkrg

T = 1c

Пример. Рассчитаем показатели переходных процессов в системе электропривода постоянного тока с регулятором частоты вращения при постоянном потоке двигателя. Индуктивность якорной цепи двигателя примем равной нулю.

Структурная схема такой системы и ЛАЧХ представлены на рис. 1-282. Эта система является системой 0-1 е коэффициентом усиления fe=9, частотой среза Wc = =9 1/с.

Расчет ведем для трех случаев.

Ступенчатое изменение задания на величину АОз=0,Шн при нулевом статическом моменте. Из (1-275) и (1-303) следует:

ДО=АОз

fe-H

1 -е

= 0,09Qh(1 - е"°)-

Время переходного процесса

=0.3 с.

ft+1

«с

Рис. 1-282. Структурные схемы и ЛАЧХ системы регулирования частоты вращения при 7я=0.

а - структурная схема замкнутой системы; б - структурная схема преобразованной разомкнутой системы регулирования; в - ЛАЧХ системы 0-1; / - усилитель и вентильный преобразователь; 2а к 26 - двигатель; 3 - тахогенератор.

Установившаяся ошибка

АОз - AQy 1

ДОз

= 0,1.

Ток двигателя определяется с помощью (1-276) и (1-302).

Если принять Гэм=1 с, /?=0,1£д,н н, где /и - номинальный ток двигателя, то получим;

днн д,н„ Айз

в начальный момент времени (/=0) бросок тока достигает недопустимого значения 9/н.

Таблица 1-35

Переходные функции системы 0-1

Реакция

Изо6ражеш1е

Оригинал

На импульс

kcOo

P+(k+l)4,o

На ступенчатое воздействие

Ошибка при линейном воздействии задания

Р + «р

Р [р + (Й+1)С0о1

fe-f 1

feWp

Линейное возрастание задания со скоростью ез=0,Шн 1/с. Из (1-278) и (1-303) находим динамический ток двигателя:

дни

-Д,Н 3

эм ,

RI ""Qnfe-fl

о.эО--»")-

OK не превосходит

Динамический ток 0,9/н.

Наброс статической нагрузки /ст=/н. Пренебрегая влиянием изменения э. д. с. двигателя при приложении возмущающего воздействия в структурной схеме рис. 1-282, разомкнем внутреннюю обратную связь по э.д.с. двигателя. При этом система трансформируется в систему типа 1 и ее передаточная функция для разомкнутого состояния

fey.n fee

= -; ис = 9 1/с. Р

Из (1-280), (1-282), (1-297) и (1-303) находим:

ток двигателя

/ = /,Л1 в-"«)=/н{1~е-«0:

изменение скорости двигателя

= 0,011(1 -e-S).

Система является статической по возмущению. Установившаяся ошибка но скорости, равная 1,1%, достигается через время

Ц = - = 0,33 с.

«с

п о-

Реакция систем второго рядка

Система 1-2 представляет собой сочетание интегрирующего и апериодического звеньев. К таким системам, например, относится следящая система с электродвигателем постоянного тока, у которого индуктивность якорной цепи принята равной нулю (рис. 1-283).

Передаточная функция разомкнутой системы 1-2

Яр (р):

«с

«с Wo

р(1+рГ) р(р-fcoo)

(1-305)

(для следящей системы на рис. 1-283 7"=

TsmJ

Обозначим m=Mo/Wc, тогда

Яр(р) =

р (p-f mwc)

(1-306)

-8 -12

•К> Н(р)

Рис. 1-283. Логарифмическая амплитудно-частотная характеристика и структурные схемы системы 1-2.

с -ЛАЧХ; 6 - структурная схема следящей системы с электродвигателем постоянного тока при =0; .81 -структурная схема той же системы в разомкнутом состоянии при =0; сФ -поток двигателя; fl - угловая скорость; G g - задаваемый путь; 6 - Путь, проходимый двигателем.

Передаточная функция замкнутой системы 1-2

Язам(р) =-

р -fmo) p-f/nw

(1-307)

Для m>4 переходные функции системы 1-2 будут иметь апериодический характер, для т< 4 -колебательный характер. Значение т-А соответствует критическому режиму, граничному между апериодическим и колебательным.

Апериодический режим (табл. 1-36). При т>4 уравнение (1-307) может быть представлено в виде

Язам(Р) =

таг:

(P+Wi) (р + ©г)

«2= Wc

т 1 f

(1-308)

(1-309)

(1-310)

В отличие от систем 1 и 0-1 значение реакции на импульс равно нулю в начальный момент времени.