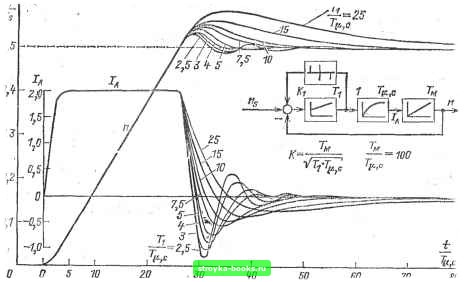Рис. 1-214. Переходная характеристика разгона под отсечку системы регулирования с

параметрами - п Ф-~ =

«8 = Ub-K

Ri Tk Ri

Rskc

0,5 D,f 0,3 D,2 0,1

0 0,2 0,6 1,0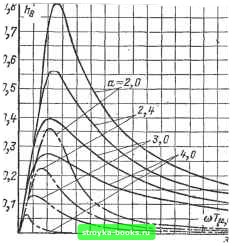

D 0,2 0,4- V,6 0,8 1,0

Рис. 1-215. Амплитудно-частотные харак- Рис. 1-216. Амплитудно-частотные характеристики теристики

и(/ш)

Rskc

система без фильтра на входе;

---. - система с фильтром на входе.

- система без фильтра на Е.ходе:

=- - система с фильтром на входе.

Увеличение К приводит к изменению низкочастотной части характеристики. При jK-oo система регулирования с ПИ-регу-лятором частоты вращения стремится к системе регулирования с П-регулятором, настроенной по модульному оптимуму. Настройка при /С = 4 соответствует настройке по симметричному оптимуму.

Для уменьшения перерегулирования частоты вращения при управлении со стороны задания на входе системы можно устанавливать фильтр.

Переходные характеристики частоты вращения для различных К при ступенчатом входном сигнале, а также для К = 4, Тф=4Г4 с показаны на рис. 1-218.

На рис. 1-219 приведены переходные характеристики ошибки по частоте вращения при ударном приложении нагрузки. Из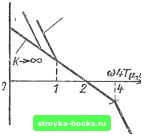

Рис. 1-217. ЛАЧХ разомкнутой системы.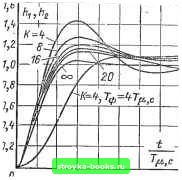

t 8 12 ie Рис. 1-218. Переходные характеристики t \

ц,с /

/12 =

R4 \ Ц.С /

при [7=const;

Ri Гэм Се Ф

при f/j,x = at.

рассмотрения характеристик видно, что с ростом К увеличивается статическая ошибка по частоте вращения, максималшая динамическая ошибка практически не меняется.

Рассмотрим еще один тип настройки системы регулирования с ПИ-регулятором частоты вращения при неизменной величине Т=4Т и различных значениях Вс

Передаточные функции разомкнутой и замкнутой систем регулирования равны:

раз,с(р) =

(1-235)

зам,с

(Р) =

(1-236)

Фазовые и частотные характеристики системы приведены на рис. 1-220.

Реакции системы на ступенчатый входной сигнал и возмущение по нагрузке, полученные на математической модели, показаны на рис. 1-221-1-223.

Случай Ti = 4 Т,. и = 6,4 Т определяет настройку на минимальную колебательность, т.е. величина резонансного пика замкнутой системы регулирования достигает минимального значения. При этом перерегулирование несколько меньше, а быстродействие несколько больше, чем при настройке по симметричному оптимуму.

Если токовый контур настроен по колебательному закону %т и в конту-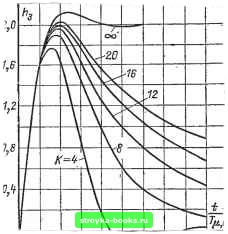

Рис. 1-219. Переходная характеристика AnfA-

Rskc

/„„ Г

при /cT=const.

ст Ц.С т (Т)

эм Се "j

Минимальная колебательность Симметричный оптимум 1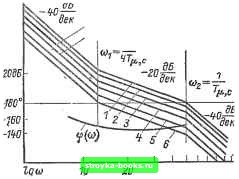

Иногда для удовлетворения технологических требований система регулирования должна обеспечивать отличный от нуля, но меньший, чем при настройке по модульному оптимуму, уровень статической просадки по частоте вращения. В этом случае регулятор частоты вращения выполняется по схеме рис. 1-224.

При апериодической настройке токового контура передаточная функция разомкнутого контура частоты вращения

30 W БО 80100

Рис. 1-220. ЛАХ и ЛФХ разомкнутой системы регулирования.

/ - в = 4Г2 ; 2 - в = 5Г2 ; 3 - В = 6,4 Г2

с Ц,с с ц,с с ц,с

(минимальная колебательность), 4 - В = 8г2

!,pas,c

Re~Rb fee 2

1+рС

Rji fej Ri RbRe

Rb+Re

(1-237)

12 tI 6-b = (t,c с

(симметричный оптимум); 5 - В = 16 Г2 .

ре частоты вращения отсутствуют дополнительные инерционности, система регулирования частоты вращения хорошо описывается уравнением четвертого порядка. В этом случае эквивалентная малая постоянная времени контура частоты вращения Г,.е=2Г .

Частотные и переходные характеристики для данной системы несколько отличаются от системы третьего порядка. Однако для практических целей можно пользоваться семействами кривых, приведенными на рис. 1-209--1-213.

Отметим, что для данного случая настройка контура частоты вращения по симметричному оптимуму соответствует настройке на минимальную колебательность.

ГэмСеФр (l+pCR,){l+Tp)

Амплитудно-частотные характеристики разомкнутого контура частоты вращения представлены на рис. 1-225.

Здесь приняты следующие обозначения:

Параметры регулятора частоты, вращения следует выбирать из условия постоян-

ства частоты среза Юср

-Тп. и неизмен-

ной длины участка ЛАЧХ 20 дБ/дек в окрестности частоты среза для возможного диапазона изменения 1<у<оо, т.е.

CRRb 1

«ср -

RM 1 R

kcRs

feT Ri ПшСеФ Ri 2Т

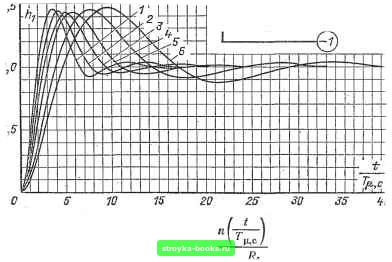Рис. 1-221. Переходная характеристика ftj =

при = const, Г5! = 4Гд.

""/sfee Обозначения - см. рис. 1-220,