
 |
|
Главная Развитие народного хозяйства [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [ 53 ] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] входного сигнала, а также прн приложении момента сопротивления приведены в [1-3, с. 288; 1-19, с. 29]. Соответствующие переходные характеристики даны на рис. 1-197. Когда система регулирования предполагает управление со стороны задания через задатчик интенсивности, преобразующий ступенчатый сигнал в линейно-возрастающий с ограничением выходного напряжения до уровня выходного напряжения задатчика, 1сривая переходного процесса может быть определена путем суммирования двух реакций системы, вызванных двумя составляющими входного сигнала. Установившееся значение приращения частоты вращения определяется из выражения для An (t) Дп(0у = /ст ТвмСеФ 4Й = Rj Rj (1-210) При настройке по модульному оптимуму контура частоты вращения получаем: An (t)y = Rs 2Tfx,c Тэт Се Ф Статическая просадка частоты вращения в системе с пропорциональным регулятором зависит от настройки системы.
Рис. 1-197. Переходные характеристики nif) . Ri 1 при t/jBx = const; Ri ПмСеФ D T 2T 13 Э Ц.Т hl=- -,14=: при -const. 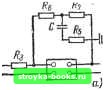
Рис 1-198. Типы исполнения пропорционально-дифференциальных регуляторов. R, + Rr 6~fep=; Tф = %Cp.T=R, + R,)Cp. Прн необходимости уменьшения уровня статической просадки частоты вращения без роста колебательности системы регулирования регулятор частоты вращения можно выполнить пропорционально-дифференциальным (ПД). Варианты исполнения регулятора приведены на рис. 1-198. Наиболее распространенный вариант регулятора, при котором ПД-звено (рис. 1-198, а) включено в прямой канал регулирования. При этом передаточная функция регулятора имеет вид: при 7ф<71. При апериодической настройке токового контура R2 1 1 т (Р) = • ~7~ Г~Г~Г Rl 7т р Н- 1 значение упреждающей составляющей регулятора принимается равным постоянной времени инерционности токового контура Т) = Тт. Постоянная Тф определяется уровнем допустимых помех в системе. Роль малой постоянной контура частоты вращения при таком выборе параметров регулятора частоты вращения играет величина Тф, а так как 7"ф<71, то усиление в контуре частоты вращения может быть существенно увеличено. При колебательной настройке токового контура ПАР)- R. 1 Rl *т 2Г2 ,р2 + 2Г.,р + 1 упреждающая постоянная регулятора выбирается равной ri = 27j T- В этом случае при заданном запасе по фазе также можно увеличить усиление. В качестве примера на рнс. 1-199 приведены ЛАЧХ рассматриваемой системы при 7ф=0,6-2Г,т- Из рисунка видно, что при одном и том же запасе по фазе усиление при наличии упреждения может быть существенно поднято (в 1,24 раза). Когда требуется быстрая отработка возмущения прн малом перерегулировании, но более медленная реакция привода на 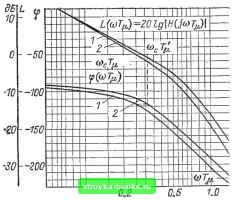 0,05 0,1 Рис. 1-199. Логарифмические амплитудно-частотные и фазо-частотные характеристики. 1 - без упреждающего звена; 2 - с упреждающим звеном. управление со стороны задания, ПД-звено может быть реализовано в канале обратной связи (рис. 1-198,6). Структура данной системы будет отличаться от ранее рассмотренной наличием фильтра на входе с псре-+Тфр даточной функцией-;----, т. е. система 1 + Т\Р замедляется. В практике эксплуатации приводов бывают случаи, когда требуется поднимать усиление в контзфе частоты вращения выше, чем при настройке по модульному оптимуму. На математической модели исследовалась схема рис. 1-192. В качестве примера брали величину VWZn,; 0,2<7<2. По результатам моделирования можно определить следующие величины: а) перерегулирование частоты вращения при ступенчатом входном сигнале (рис. 1-200); б) Перерегулирование динамического тока при линейном входном сигнале (рис. 1-200);" в) время достижения первого установившегося значения Лу выходной величины (рис. 1-201) практически ti мало зависит от у. Здесь у - -у"--параметр семейст- ва кривых; г) максимальное значение якорного тока при ступенчатом входном сигнале в за- висимости от настройки системы (рис. 1-202). Практически 1шах не зависит от у. Кривые рис. 1-200 позволяют для заданного значения у, задаваясь перерегулированием б, определить коэффициент усиления контура частоты вращения из выражения Ri Rj feT УзмСеФ Ro.c Ri fee 60 20 ID 12 Щ 1& Рис. 1-200. Зависимость перерегулирования выходной величины от настройки системы для различных соотношений постоянных Y=?ф,e/27.т• 24 20 16 12 8 Ч г Ч- в S 1Q. 12 W Рис, 1-201. Область изменения времени достижения первого установившегося значения tvs выходной величины в зависимости от настройки системы при ступенчатом сигнале f/nx- 2,0 1,6 0,8 0,4
2 Ч Б 8 10 12 П Рис. 1-202, Область изменения максимального значения выходной величины в зависимости от настройки системы. На рнс. 1-203 приведены частотные характеристики замкнутой системы регу.чи-рования для частоты вращения и тока якоря, определяемые выражениями: и (/со) (1-212) Ubx (/w) Rskn (1-213) Зависимости (1-212) и (1-213) позволяют определить уровень пульсаций якорного тока и частоты вращения привода, вызванных синусоидальными помехами входного сигнала и тахогенератора, причем при определении пульсаций тока и частоты вращения, вызванных помехами тахогенератора, в (1-212) и (1-213) значение Ra должно быть заменено на Rt, т. е. RJR,= 1. Влияние э. д. с. двигателя на динамику токового контура. При анализе систем подчиненного регулировагшя обычно пренебрегают влиянием э. д. с. двигателя на процессы в токовом контуре, что позволяет су-гцественно упростить расчет системы регулирования. -0,5 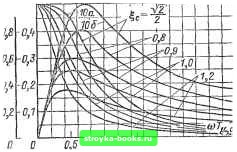 1,0 1,5 2,0 г,5 3,0 Рис. 1-203. Амплитудно-частотные характеристики для тока и частоты вращения 1оа - пЦ<£>) Rskc tux(/w) Количественная оценка влияния э. д. с. двигателя может быть получена из анализа передаточной функции токового контура с учетом цепи э. д. с: в разомкнутом состоянии H{p)Hi{p)Hn{p) = R.CRP( + T,.P) Гэм Гэ Р" + ГэмР где Hi{p)== Гэм7эрН-ГдмР+ 1 fee RpO-,.p) (1-214) переда- точная функция разомкнутого контура без учета влияния э. д. с. двигателя; Яп(р) = ТэмТэР- + ПР+1 -поправка. учитывающая влияние э. д. с. двигателя; в замкнутом состоянии Hsau,T (Р) = (1 + Пр) 1 + ; (1-215) Здесь BT,= {CR2Ra)/(kBkr) - эквивалентная постоянная времени интегрирования токового контура; обычно Вт>27 .j,. Подробно влияние э. д. с. на основе приведенных соотношений рассмотрено в [1-19, с. 86]. На рис. 1-204, а-1-207, а приведены переходные процессы токового контура при ступенчатом задании с учетом влияния э. д. с. двигателя. На рис 1-204, б, в - 1-207, б, в, показана реакция якорного тока и частоты вращения на ступенчатый входной сигнал с учетом влияния э. д. с. двигателя. На рисунках / f при /з-const; [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [ 53 ] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] 0.002 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||