
 |
|
Главная Развитие народного хозяйства [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [ 52 ] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] Регултор частоты Регулятор Вращения (PC) тош (РТ) 4--Ч У с R. > 0,7- Прворазо-Ватель Двигатель постоянного тока, I------- Ri Яг > Тф1р + 1 Rc(T,p+l) Датчик токе t- - Тф,тр+1 iCefp Датчик скорости Тф,ср+1 Рис. 1-192. Структурная схема двухконтурной системы регулирования с пропорциональным регулятором частоты вращения. чения пульсаций выходного напряягения до уровня, при котором система фазового управления преобразователя работает без сбоев; пульсации якорного тока и частоты вращения находятся в допустимых пределах, и аналоговые усилители работают без заметного снижения коэффициента усиления. Рассматриваются такие соотношения между параметрами токового контура, при которых влияние э.д.с. двигателя существенно не сказывается на динамике процессов. Оценка соответствующих параметров будет дана ниже. Настройка параметров регулятора тока производится по формулам CRo.T = (1-197) Ci?,= B,-%, (1-198) где Вт - эквивалентная постоянная интегрирования токового контура; Тв - электромагнитная постоянная времени якорной цепи. С учетом того, что в рассматриваемой полосе пропускания частот звено чистого запаздывания может быть аппроксимировано апериодическим звеном 1/(Ц-тр), величина бо,т при настройке контура тока по модульному оптимуму определяется (см. Во,1 = Тр.т + Tфf -\- Гфд, -\-х + (1-199) Эквивалентная малая постоянная времени контура тока равна: Т - Во,т - Тф, в упрошенном- варианте расчета, которым часто пользуются на практике, под 7", понимается сумма малых постоянных времени в прямом и обратном каналах контура тока. При этом -2Тп Когда сумма малых постоянных врем-е-ни фильтров удовлетворяет условию -(7Р,т + 7ф1 + ад<2, чистое запаздывание преобразователя т в выражениях для Т. не учитывается, т. е. систему сеточного управления и преобразователь представляют как безынерционное пропорциональное звено. При этом неуправляемость вентиля во время его проводимости компенсируется прн отпирании следующего вентиля, так как ошибка регулирования непрерывно интегрируется регулятором тока. Здесь т - число фаз выпрямителя тока, fc - частота питающей сети. Необходимо отметить, что в связи с внедрением систем регулирования с раздельным управлением реверсивных преобразователей, а также с применением новой элементной базы - интегральных операционных усилителей - имеют место и другие структуры токового контура и регулятора тока. Этн специальные схемы рассмотрены в других параграфах. Из опытных данных, полученных при наладке систем подчиненного регулирования, изготовленных на заводах электропромышленности до 1978 г., малая постоянная токового контура 5-8 мс. Передаточная функция токового контура при настройке по модульному оптимуму равна; Ят (Р) = 2Т1У + 2Т.р+\ :(1-200) В этом случае реагщия контура тока на скачок входного сигнала характеризуется перерегулированием примерно 4,3% и временем нарастания выходной величины до первого установившегося значения При коэффициентах усиления, меньших, чем при настройке по модульному оптимуму, передаточная функция токового контура имеет вид: Ri I (1-201) Здесь -* 7ф,т Отметим, что настройке контура тока по модульному оптимуму соответствует коэффициент демпфирования При практической реализации токового контура коэффициент усиления регулятора тока обычно загрубляют, что соответствует т>У2/2. В этом случае передаточную функцию токового контура можно представить инерционным звеном. Нт (Р) Вр+\ В общем случае контур частоты вращения описывается уравнением высокого порядка. Однако при коэффициентах усиления регулятора частоты вращения меньших, чем прн настройке по модульному оптимуму, для практических целей можно пользоваться приближением второго порядка. Передаточная функция замкнутого контура частоты вращения записывается в виде зам (р) = т, = Ч-ЙР-Ы где Вг. - эквивалентная постоянная интегрирования контура частоты вращения: И - частота вращения, об/мин; Ф -магнитный поток одного полюса двигателя, Вб; Се - электрическая постоянная двига-1 pN теля: се=----=0,105 сш; сш -механи- ЬО а 1 pN ческая постоянная двнгателя;См =--; 2л а р -число пар главных полюсов; N - число проводников на якоре; а - число пар параллельных ветвей якоря; Гам--электро- механическая постоянная времени привода; Tjc - эквивалентная малая постоянная времени контура частоты вращения: r,x,c = rp,c-b2r,t-fr$,c. (1-203) Затухание переходного процесса в контуре частоты вращения характеризуется коэффициентом демпфирования J ]/ i 2 V V (1-204) Настройке контура частоты вращения по модульному оптимуму соответствуют следующие значения: зам (Р) = Вс = 2Гц,с; п Ri 2Г ,р22Г,еР-Ы Передаточные функции замкнутой системы регулирования для 12/2 равны: п(р) t/ex(p) 1 Ra-kc Hp) ЯПмСеФр (1-205) /2(P) = t/вх (P) 1 RakcRs ie.Tlp + ifTp + l Из ip) = I Hp) /ст (p) 4gr,cPH-4gr,cP+l (1-206) (1-207) В формулах Гф.с - постоянная времени фильтра в цепи обратной связи контура частоты вращения; /ст -ток статической нагрузки; An - динамическая просадка частоты вращения при приложении статической нагрузки (момента сопротивления); Яар)= = -:гХ /ст(Р) ТэшСеФ 4gg7.c(l+VP) 4g7.cPH-4r.cPH-l (1-208) Изображения и оригиналы . выражений тока и частоты вращения для системы второго порядка при подаче на вход контура частоты вращения ступенчатого и линейного входного сигналов, а также при приложении момента сопротивления приведены в [1-3, с. 284; 1-19, с. 25]. Соответствующие им переходные характеристики показаны на рис. 1-193 - 1-196. 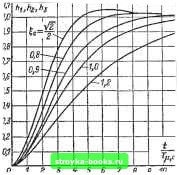 Рис, 1-193. Переходные характеристики n{t) при t/bx=const; Яз fee i?4 1 ТшСеФ при == a. Яз fee ha - при = const. 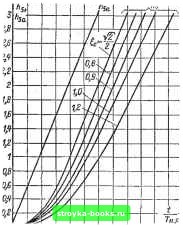 Рис. 1-194, Переходные характеристики n(t) ft5 = /?4 1 /?2- fee при вх = ha~0T- - приведенное значение вход-Ц.С ного сигнала. 11*
Рис. 1-195. Переходная характеристика , ПО 3 fee-э Ус л77- при ех = const. ивхЯПиСеФ
Рис. 1-196. Переходная характеристика An (ЛТэшСеФ , = const. При настройке токового контура и контура частоты вращения по модульному оптимуму, а также при отсутствии каких-либо дополнительных инерционьюстей в контуре частоты вращения контур частоты вращения описывается уравнением третьего порядка. Передаточная функция замкнутой системы регулирования при этом имеет вид: t/вх (Р) Rskc (1-209) Изображения и оригиналы выражений тока и частоты вращения для системы третьего порядка при подаче ступенчатого [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [ 52 ] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] 0.0014 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||