
 |
|
Главная Развитие народного хозяйства [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [ 51 ] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] При этом оптимизированная передаточная фшкция контура Переходный процесс характеризуется перерегулированием 4,37о и временем первого достижения установившегося значения, равным 4,7 7" • В рассмотренном примере объект регулирования содеряшт одну большую постоянную времени. В общем случае объект регулирования может быть более сложен, т. е. содержать несколько инерционностей, форсирующие, интегрирующие и другие звенья. Их компенсация осуществляется соответственно более сложным регулятором. Принцип компенсации состоит в том, что каждому звену объекта регулирования должно соответствовать звено с обратной передаточной функцией в составе регулятора. На практике часто в прямом канале регулирования имеется несколько малых не-компенсируемых постоянных времени, которые могут быть как действительными, так и комплексно-сопряженными, что соответствует наличию колебательных звеньев второго порядка. В этом случае оптимальная эквивалентная постоянная интегрирования равна удвоенной сумме этих малых постоянных к времени, т. е. Во=22 ц/ • Передаточная функция в этом случае с достаточной для практических расчетов точностью может быть описана уравнением второго порядка --- . • Tl,p + 2Tp + l i=i (=1 Далее рассмотрим наиболее сложный случай, когда малые инерционности и упреждения имеются в канале прямой и обратной связи (рис. 1-188). Большая постоянная времени считается скомпенсированной. Критерием выбора £0=1/123 будет условие равенства нулю первых трех производных от модуля передаточной функции по угловой частоте при стремлении ее к нулю. При этом "г q k 3i=l 4{=1 1,-=1 2»=1 * 3,=1 4,=1 1<=1 21=1 4/=1 21=1 Физический смысл этого критерия состоит в том, что- чем больше числопроиз- водных при ю=0 равны нулю, тем набольшем диапазоне частот амплитудно-частотная характеристика будет приближаться к горизонтальной линии и тем более быстродействующей будет система регулирования. В рассматриваемой системе определяется один параметр - коэффициент усиления регулятора, поэтому для его определе- 1<зП(Тг1Р + 1) Рис. 1-188. Обобщенная структурная схема контура с одним интегральным звеном, где П -символ произведения, m>fe, 9>/". ния достаточно условия равенства нулю только второй производной. Все нечетные производные равны нулю при любом значении В. Когда система регулирования содержит не один параметр, а несколько, то для расчета настройки регулятора используется условие равенства нулю четных производных более высокого порядка в соответствии с числом определяемых параметров. Этот критерий оптимизации получил название модульного оптимума. Следует отметить, что рассмотренные расчеты более простых структур можно получить из общей формулировки в виде частных случаев. Аппрокскмкрованное значение оптимальной передаточной функции замкнутой системы рис. 1-188 имеет внд: Я2(Р) = 2Т1г + 2Тр+1 Во + 2j - 2 4г 2i=l 4j=l - эквивалентная малая постоянная времени разомкнутого контура регулирования. При этом коэффициент относительного демпфирования 2Т.. 2 Vk 2 = - = 0,707. Для выбора регулятора последующего контура этот уже оптимизированный контур с достаточной для практических расчетов точностью аппроксимируется как инерционное звено с постоянной времёни;ав-* ной удвоенной эквивалентной малой постоянной времени оптимизированного контура (Укз)/12Т р+1), и рассматривается как составная часть объекта. Настройка параметров регулятора рассчитывается аналогично по модульному оптимуму, изложенному выше. В качестве примера настройки по модульному оптимуму рассмотрим многоконтурную систему, где собственный объект регулирования 1-то контура (за исключением г=1) не содержит малых (нескомнен-сированных) постоянных времени. В этом случае соотношение между эквивалентными малыми постоянными времени последующего и предыдущего контуров равно 2, т. е. Оптимизированная передаточная функция г-го контура i/ki и -1) i + ... + 2iT,,p-\-l На рис. 1-189 приведены кривые реакции систем второго - пятого порядка иа единичный ступенчатый сигнал, оптимизированных указанным образом. Кривые построены в функции относительного времени mTi {2Т 1=6). Из рассмотрения кривых следует, что характер некоторых процессов мало меняется с увеличением числа контуров. Поэтому допустимо определять характер переходного процесса системы с большим числом контуров по усеченному уравнению третьего порядка, а в большинстве практические; случ1ев и второго порядка. Усеченное уравнение получается при отбрасывании членов порядка соответственно выше третьего или второго. Погрешность, получаемую при этом, можно оценить, со-1Юставляя фактическую кривую переходного процесса с кривой 2 или /. Рассмотренный выше критерий оптимизации, известный под названием «модульный оптимум», в иностранной практике как «Betrags-optimum», получил широкое распространение благодаря простоте расчета и реализации при хорошем качестве регулирования. Симметричный оптимум. Другой типовой критерий оптимизации распространяется на контуры, содержащие два интегральных звена (рнс. 1-190) или одно интегральное и одно инерционное звено в объекте регулирования при достаточно большой постоянной времени To>47j. Обычно одно интегральное звено вводится в состав регулятора, а второе принадлежит объекту регулирования. В этом случае pji получения устойчивой системы в регудя.Щл 1,00 0,75 0,50 0,25
г,5 5,0 7,5 Рис. 1-189. Кривые реакции системы подчиненного регулирования на скачок управляющего воздействия. 1 - реакция контура второго порядка; 2 - реакция контура третьего порядка; 3 - реакция контура четвертого порядка; 4! - реакция контура пятого порядка; <р=4,1б; рЗ.Ббб; <рз=3.4(5; t =3,86, где Ь=iT , . р4 II. ре должно быть дифференцирующее звено. Такая структура часто используется , для получения астатических характеристик по возмущению Хзг (рнс. 1-190) или для других специальных случаев, например для уменьшения влияния колебаний сетевого напрялсения на колебания тока в системе подчиненного регулирования. Передаточная функция замкнутой системы будет равна: Пзаш{р) = ВрП (Тг р + 1)-f Гр-fl вида Н. Рассмотрим зам iP) = - передаточную функцию I 1=/г ВрП (ГгР+ l)-frp+ 1 Эти передаточные функции характеризуются одинаковым затуханием переходного процесса. Определим это затухание из условия модульного оптимума, т. е. величины, S и Т должны ви0ираться так, что-бц,(Цррв,ые„.четыре производные,, от модуля Регулятор Объект регулирования
Рис. 1-190. Структурная схема контура с двумя интегральными звеньями. передаточной функции Н но угловой частоте были равны нулю при стремлении последней к нулю. Из этих условий следует: В=8 (2 Tj) и Г=42 Тг. Введем обозначения 2 *~ц • да оптимизированная передаточная функция имеет вид: Н /n 4Г Р+1 "зам.оп \Р)--о-5--п- . 8ТЗрН8Г2р2+4Гр+1 Такая настройка регулятора известна под названием «симметричный оптимум», так как при этом фазовые и амплитудные характеристики разомкнутого контура симметричны относительно частоты среза (рис. 1-191). Переходный процесс характеризуется перерегулированием А3% и временем первого достижения установившегося значения 3,1 . Следует отметить, если малые инерци-онности 2 7"i,o содержатся также и в ка- 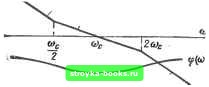 fO SB/den 2D дБ/дек ч-ОдВ/ден Рис. 1-191. ЛАЧХ оптимизированного но симметричному критерию контура. нале обратной связи, то их можно просуммировать с малыми инерционностями прямого канала регулирования. В этом случае с точностью, достаточной для практических расчетов, =2 + S Ti,o- При оптимизации последующего контура системы регулирования на входе внутреннего контура, настроенного по симмет- ричному оптимуму, устанавливается фильтр с постоянной времени 47 ,т. е. инерционное звено 1/(471 p+l). При этом передаточная функция этого контфа с фильтром имеет вид; J При оптимизации последующего контура системы регулирования передаточная функция Н,Хр) аппроксимируется как инерционное звено- 1/(47 р-1-1). В этом параграфе изложены два наиболее простых распространенных критерия оптимизации Применяются и другие настройки регуляторов. Некоторые из них рассматриваются в следующих параграфах. 1-43. ОДНОКРАТНОИНТЕГРИРУЮЩАЯ СИСТЕМА РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ В СИСТЕМЕ ВЕНТИЛЬНЫЙ ПРЕОБРАЗОВАТЕЛЬ - ДВИГАТЕЛЬ ПОСТОЯННОГО ТОКА Система регулирования с пропорциональным регулятором скорости электропривода (частоты вращения электродвигателя) получила наиболее широкое распространение в промышленности и применяется для электроприводов, допускающих по технологическим требованиям астатическую характеристику по входному воздействию и статическую по возмущающему. К таким приводам относятся, в частности, разнообразные механизмы прокатного производства, например летучие ножницы, главные приводы, нажимные устройства чистовой и черновой клетей, намоточные устройства. Структурная схема системы регулирования с пропорциональным регулятором частоты вращения приведена на рис. 1- 92. Система регулирования состоит из двух контуров: внутреннего (контура тока) и внешнего (контура частоты вращения). В качестве регуляторов и датчиков используются операционные усилители. Регулятор тока выбирается интегрально-пропорциональным, дифференцирующая часть которого компенсирует электромагнитную постоянную времени объекта регулирования, а интегрирующая часть обеспечивает заданное качество процессов регулирования. Регулятор частоты вращения выбирается пропорциональным. Ограничение тока якорной цепи достигается путем ограничения выходной величины регулятора частоты вращения, являющейся заданием на ток. Анализ выполняется при следующих предпосылках: ток якорной цепи является непрерывным и внешняя характеристика преобразователя не имеет изломов при малых токах, не учитывается поток реакции якоря; фильтры датчиков тока и частоты вращения выбираются из условия ограни- [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [ 51 ] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] 0.0015 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||