ПРИМЕР: Чему равен импеданс цепи, содержащей резистор сопротивлением 220 ом, соединенный последовательно с конденсатором, имеющим емкостное реактивное сопротивление 270 ом?

Дано: Решение:

R = 220 Ом = +

Х = 270 Ом. = (220) + (270) = 121300

Z = л/121300 = 348,280м.

Z = 348,28 Ом.

Если последовательная цепь содержит индуктивное и емкостное реактивные сопротивления, а также активное сопротивление, необходимо найти полное реактивное сопротивление (X). Реактивное сопротивление может быть либо индуктивным, либо емкостным. Следовательно, может быть использована одна из следующих формул:

= R + Х;

Z =R+X.

17-2. Вопросы

1. Как называется полное противодействие в цепи переменного тока?

2. Какая формула используется для вычисления величины полного противодействия в последовательной цепи?

3. Чему равно значение Z в последовательной цепи переменного тока, где Х = 3 Ом, Х; = 6 Ом, а R = 4 Ом?

17-3 ЗАКОН ОМА

Закон Ома не может быть применен в цепях переменного тока потому, что он не учитывает реактивное сопротивление. Модифицируя закон Ома путем учета импеданса, можно полушть общий закон, который применим к цепям переменного тока.

I = преобразуется в I = . R Z

Z 519,71 I = 0,23 А или 230 мА.

17-3. Вопросы

1. Каким образом модифицируется закон Ома, чтобы его можно было применить к цепям переменного тока для определения напряжения и тока?

2. Последовательная цепь содержит резистор сопротивлением 510 ом, индуктивное сопротивление 300 ом и емкостное сопротивление 375 ом. Какой ток течет по цепи, если к ней приложено напряжение 120 вольт?

17-4. ЦЕПИ RLC

Материал, изложенный до сих пор, применим ко всем цепям переменного тока. В приведенных примерах рассматривались последовательные цепи. Понятия, рассмотренные в этом параграфе, не содержат нового материала, но используют все принципы, изложенные ранее.

Эта формула применима к переменному току, текущему в любой цепи.

ПРИМЕР: Последовательная цепь содержит резистор сопротивлением 510 ом, индуктивное сопротивление 250 ом и емкостное сопротивление 150 ом. Какой ток течет по гепи, если к ней приложено напряжение 120 вольт?

Дано: Решение:

R = 510 Ом X = X, + Х

Xj = 250 Om Х = 250 - 150

Хр = 150 Ом X = 100 Ом (индуктивное)

Е = 120В Z=R+X

Z =(510) +(100)

Z = л/270100 Z = 519,71 Ом Е 120

ПРИМЕР: Парис. 17-5 показана последовательная RLC цепь. Необходимо вычислить Х, Xj, X, Z и 1,. Сначала вычислим Х Дано: f = 60 Гц

X, и X. Решение:

С = 470 мкФ L = 27 мГн.

Хс =

Хс =

27ifC

(6,28)(60)(0,000470) Х = 5,65 Ом

Xj = 2nth

= (6,28)(60)(0,027) = 10,17 Ом X = Xc-Xj= 10,17- 5,65 X = 4,52 Ом (индуктивное). Используем значение X для вычисления Z. Дано: Решение:

X = 4,52 Ом Z2 = R2 +

R = 10 Ом. Z2 = (10)2 + (4,52)2 = 120,43

Z = Vl20,43 = 10,97 Ом.

Это значение Z может быть использовано для вычисления полного тока (Ij,).

Решение:

Дано: Z = 10,97 Ом Е = 120 В.

1т = - =

Е 120

Z 10,97 = 10,94 А.

Е-120 в, f-60 Гц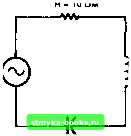

С - 470 мкФ

L = 27 мГн

Рис. 17-5. Последовательная цепь RLC.