
 |
|
Главная Введение в электрику [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [ 73 ] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] [170] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] [190] [191] [192] [193] [194] [195] [196] [197] [198] [199] [200] [201] [202] [203] [204] [205] [206] [207] [208] [209] [210] [211] как и использование эквивалентных значений постоянного тока и напряжения. • Эффективные значения являются наиболее широко используемыми значениями, полученными при измерениях. • Закон Ома можно использовать и для эффективных значений. • Значения переменного тока и напряжения предполагаются эффективными, если не оговорено другое. Глава 14. САМОПРОВЕРКА 1. Каково фазовое соотношение между током и напряжением в чисто резистивной цепи ? 2. Каково эффективное значение напряжения в цепи переменного тока, в которой течет ток 25 мА через сопротивление 4,7 кОм ? 3. Каково падение напряжения на двух резисторах 4,7 кОм и 3,9 кОм, соединенных последовательно в цепи переменного тока при приложенном напряжении 12 вольт? 4. Чему равен ток через каждый из резисторов 2,2 кОм и 5,6 кОм, соединенных параллельно при приложенном к ним переменном напряжении 120 вольт? 5. Что определяет потребление мощности в цепи переменного тока? 6. Чему равна потребляемая мощность в цепи переменного тока, в которой напряжение 120 вольт приложено к нагрузке 1200 Ом? Глава 15. ЕМКОСТНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА ЦЕЛИ После изучения этой главы студент должен быть в состоянии: • Описать фазовое соотношение между током и напряжением в емкостной цепи переменного тока. • Дать определение емкостного сопротивления (реактивного сопротивления емкости) в емкостной цени переменного тока. • Описать, как резистивно-емкостные цепи могут использоваться для фильтрации, в качестве элементов согласования и фазового сдвига. • Объяснить как работают RC фильтры верхних и нижних частот. Конденсаторы являются ключевыми компонентами цепей переменного тока. Конденсаторы вместе с резисторами и катушками индуктивности образуют полезные электронные цени. 15-1. КОНДЕНСАТОРЫ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА Когда к конденсатору прикладывается переменное напряжение, создается впечатление, что во всей цепи есть поток электронов. Однако, электроны не проходят через диэлектрик конденсатора. При увеличении и уменьшении амплитуды переменного тока конденсатор заряжается и разряжается. Результирующее движение электронов от одной обкладки к другой представляет ток. В емкостной цепи переменного тока фазовое соотношение между током и приложенным напряжением не такое, как в чисто резистивной цени. В чисто резистивной цени ток находится в фазе с приложенным напряжением. В емкостной цепи переменного тока ток и напряжение нахо- 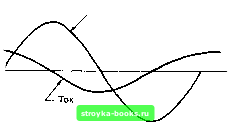 Напряжение Рис. 15-1. Обратите внимание на то, что ток и напряжение в емкостной цепи переменного тока находятся не в фазе. Ток опережает приложенное напряжение. дятся не в фазе друг с другом (рис. 15-1). Когда ток максимален, напряжение равно нулю. Это соотношение обус--ловлено сдвигом по фазе на 90 градусов. В емкостной цепи ток опережает приложенное напряжение. В емкостной цепи переменного тока приложенное напряжение постоянно изменяется, вынуждая конденсатор , заряжаться и разряжаться. После того как конденсатор цервоначально зарядится, напряжение на его обкладках противодействует любому изменению приложенного напря-,жения. Противодействие, которое конденсатор оказывает 1 приложенному переменному напряжению, называется емкостным сопротивлением. Емкостное сопротивление обозначается и измеряется в омах. Емкостное сопротивление может быть вычислено по формуле: ~ 27rfC где 7г = 3,14, f - частота в герцах, С - емкость в фарадах. Емкостное сопротивление является функцией частоты приложенного переменного напряжения и емкости. Увеличение частоты уменьшает емкостное сопротивление, что приводит к возрастанию тока. Уменьшение частоты увеличивает противодействие и приводит к уменьшению тока. ПРИМЕР: Чему равно емкостное сопротивление конденсатора емкостью в 1 микрофараду при частоте 60 герц? Дано: Решение: 7г = 3,14 27rfC 8. 61 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [ 73 ] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] [170] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] [190] [191] [192] [193] [194] [195] [196] [197] [198] [199] [200] [201] [202] [203] [204] [205] [206] [207] [208] [209] [210] [211] 0.0015 |