
 |
|
Главная Введение в электрику [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [ 29 ] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] [170] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] [190] [191] [192] [193] [194] [195] [196] [197] [198] [199] [200] [201] [202] [203] [204] [205] [206] [207] [208] [209] [210] [211] 91 Гпава 5 = 2000 Ом. 1 1 1 Ra 1000 2000 2000 Кд - - 3 R = 666,67 Ом. Теперь найдем эквивалентное сопротивление (R) резисторов R, Rj и Rg. Сначала найдем общее сопротивление (Rg) последовательно соединенных резисторов R и R. Дано: Решение: Rg = ? Rg = Rg + Rg Rg = 1500 OM Rg = 1500 + 3300 = 4800 Ом. Rg = 3300 Ом. Дано: Решение: R = 4700 Om Rb R4 Rs R= 4800 Ом. (В этом случае s общий знаме- 111 натель найти +-сложно. Rb 4700 4800 Будем использовать десятичные дроби.) = 0,000213 + 0,000208 Rb Rb = 0,000421 Rg = 2375,30 Ом. Нарисуем эквивалентную цепь, подставляя R и R, и найдем полное сопротивление последовательной эквивалентной цепи. См. рис. 5-20. - Ет= 120 В = 666,67 0м Вд=5,6к0м = 2375,3 0м -w.- Рис. 5-20 = 120 В Rt 8641,97 R = 8641,97 Ом. 1 = 0,0139 А или 13,9 мА. В последовательной цепи по всей цепи протекает одинаковый ток. Следовательно, ток, протекающий через R3, равен общему току в цепи. =I,j, =13,9мА. 5-3. Вопросы 1. Запишите формулы, необходимые для определения полного тока в последовательной и параллельной цепях, когда известны токи, протекающие через отдельные компоненты. 2. Запишите формулы, необходимые для определения полного напряжения в последовательной и параллельной цепях, когда известны падения напряжения на отдельных участках. 3. Запишите формулы для определения полного сопротивления последовательной и параллельной цепей, когда известны отдельные сопротивления. 4. Запишите формулы для вычисления полного тока, напряжения или сопротивления в последовательной или параллельной цепях, когда хотя бы две из трех величин (ток, напряжение и сопротивление) известны. Дано: Решение: R, = ? К, = К + Кз + Кз = 666,67 Ом = 666,67 + 5600 + 2375,30 R3 = 5600 Om R = 8641,97 Ом. Rg = 2375,30 Ом. Теперь с помощью закона Ома найдем общий ток в эквивалентной цепи. Дано: Решение: 1, = ? т .bl- 5. Чему равен общий ток в цепи, изображенной на рис. 5-21? = 12 в = 500 Ом Rj = 1200 Ом Rj = 2200 Ом. -Wr- Еу = 12 В 500 Ом Rj -1200 0м 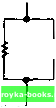 : «3 = 2200 Ом Рис. 5-21. РЕЗЮМЕ Электрическая цепь состоит из источника тока, нагрузки и проводника. Путь тока в электрической цепи может быть последовательным, параллельным или последовательно-параллельным. Последовательная цепь предоставляет только один путь для протекания тока. Параллельная цепь предоставляет несколько путей для протекания тока. Последовательно-параллельная цепь обеспечивает комбинацию последовательных и параллельных путей для протекания тока. Ток электронов протекает от отрицательного вывода источника тока через нагрузку к положительному выводу источника тока. Протекающий в электрической цепи ток можно изменять путем изменения либо напряжения, либо сопротивления. Закон Ома связывает между собой силу тока, напряжение и сопротивление. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [ 29 ] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] [170] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] [190] [191] [192] [193] [194] [195] [196] [197] [198] [199] [200] [201] [202] [203] [204] [205] [206] [207] [208] [209] [210] [211] 0.0015 |