
 |
|
Главная Введение в электрику [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] [ 170 ] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] [190] [191] [192] [193] [194] [195] [196] [197] [198] [199] [200] [201] [202] [203] [204] [205] [206] [207] [208] [209] [210] [211] Шаг 2. Нанесем логические функции, помечая их знаком X в соответствующем квадрате. АВ + АВ + АВ Первое Второе Третье слагаемое слагаемое слагаемое Пометим первое Пометим второе слагаемое А В. слагаемое AR Шаг 3. Объединим соседние квадраты, помеченные знаком X, в наибольшие возможные группы. Проанализируем диаграмму -- какая возможна наибольшая группа? Наибольшая возможная группа состоит из двух квадратов. Пометим третье слагаемое AR 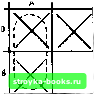 Одна из возможных групп показана штриховой линией. Другая возможная группа на этой диаграмме показана штриховой линией. Шаг 4. Логически сложим эти группы (операция ИЛИ): или А, или В = А + В. Шаг 5. Упрощенным выражением для АВ + АВ + АВ = Y является А + В = У, что получено из диаграммы Вейча. ПРИМЕР: Найдите упрощенное выражение для ABC + ABC + ABC + ABC = Y. Шаг 1. Нарисуем диаграмму Вейча для трех неременных. 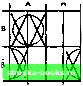 с с с Шаг 3. Объединим соседние квадраты в наибольшие возможные группы. с с с Шаг 2. Пометим знаком X логические функции каждого слагаемого на диаграмме Вейча. Шаг 4. Запишем слагаемые для каждой петли, одно слагаемое на каждую петлю: АВ, ВС Шаг 5. Упрощенным вьфажением является АВ + ВС = Y. Отметим необычное объединение двух нижних квадратов. Четыре угла диаграммы Вейча считаются связанными, как если бы диаграмма была свернута в шар. ПРИМЕР: Найдите упрощенное выражение для: ABCD + ABCD + ABCD + ABCD + ABCD + ABCD = Y. Шаг 1. Нарисуем диаграмму Вейча для трех переменных. 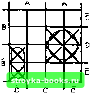 •Шаг 2. Пометим знаком X Шаг 3. Объединим сосед-логические функции каждого ние квадраты в наиболь-слагаемого на диаграмме шие возможные группы. Вейча. Шаг 4. Запишем слагаемые для каждой петли, одно слагаемое на каждую петлю: AD, ABC. Шаг 5. Для получения упрощенногоыражения логически сложим полученные слагаемые: AD + ABC = Y. 33-1. Вопросы 1. Какова функция диаграмм Вейча? 2. Сколько переменных может быть представлено на диаграмме Вейча? 3. Перечислите шаги при использовании диаграммы Вейча. 4. Упростите следующие выражения с помощью диаграмм Вейча. а. ABC + АБС + АБС + ABC + ABC = Y. б. ABCD + АВШ + ABCD-f ABCD + ABCD+ ABCD + ABCD = Y. B. AB + ABD + BCD + ВС + ABCD = Y. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] [ 170 ] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] [190] [191] [192] [193] [194] [195] [196] [197] [198] [199] [200] [201] [202] [203] [204] [205] [206] [207] [208] [209] [210] [211] 0.0015 |