
 |
|
Главная Введение в электрику [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [ 166 ] [167] [168] [169] [170] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] [190] [191] [192] [193] [194] [195] [196] [197] [198] [199] [200] [201] [202] [203] [204] [205] [206] [207] [208] [209] [210] [211] ~ у ABCD > Y-ABC ABCDEFGH Рис. 32-1. Логические обозначения элемента И.
Рис. 32-2. Таблица истинности для двухвхо-дового элемента И. обозначения представляют наиболее часто используемые элементы с двумя, тремя, четырьмя и восемью входами. Работу элемента И отражает таблица на рис. 32-2. Такая таблица, называемая таблицей истинности, показывает выходное состояние элемента для любых возможных состояний входов. Входы обозначены А и В. Выход обозначен Y. Обш;ее число возможных комбинаций в таблице истинности определяется следуюш;ей формулой: N = 2", где N - обш;ее количество возможных комбинаций, п --обш;ее число входных переменных. ПРИМЕР: Для двух входных переменных N = 2 = 4. Для трех входных переменных N = 2 = 8. Для четырех входных переменных N = 2 = 16. Для восьми входных переменных N = 2 = 256. Элемент И выполняет операцию логического умножения. Логическое умножение известно как функция И. Выход элемента И математически может быть представлен равенством Y = А А В или Y = АВ. Функция И - точка между двумя переменными А и В. 32-1. Вопросы 2. Нарисуйте схематическое обозначение, используемое для элемента И с двумя входами. 3. Изобразите таблицу истинности для элемента И с тремя входами. 4. Какую логическую операцию выполняет элемент И? 5. Как алгебраически изображается операция, выполняемая элементом И? 32-2. ЭЛЕМЕНТ ИЛИ На выходе элемента ИЛИ появляется 1, если на любой из его входов подана 1. На его выходе появляется О, если на все его входы поданы 0. Значения на выходе элемента ИЛИ с двумя входами приведены в таблице истинности на рис. 32-3. Общее число возможных комбинаций выражается форгулой N = 2 = 4. В таблице истинности приведены все четыре комбинации. Элемент ИЛИ выполняет логическую операцию сложения. Алгебраически операция, выполняемая элементом ИЛИ, выражается следующим образом Y = А -Ь В или Y = А V В. Знак плюс обозначает функцию ИЛИ. На рис. 32-4 изображены логические обозначения для элемента ИЛИ. Входы обозначены А и В, а выход обозначен Y. Элемент ИЛИ может иметь любое число входов, большее одного. На рисунке изображены элементы ИЛИ с двумя, тремя, четырьмя и восемью входами. 32-2. Вопросы 1. При каких условиях на выходе элемента ИЛИ появляется 1? 2. Нарисуйте схематическое обозначение, используемое для элемента ИЛИ с двумя входами. 3. Изобразите таблицу истинности для элемента ИЛИ с тремя входами. 4. Какую логическую операцию выполняет элемент ИЛИ? 5. Как алгебраически изображается операция, выполняемая элементом ИЛИ?
А+В+С Рис. 32-3. Таблица истинности для двухвходо-вого элемента ИЛИ. А+В+С+[>+ E+F+G+H Рис. 32-4. Логические обозначения элемента ИЛИ. 32-3. ЭЛЕМЕНТ НЕ Простейшей логической цепью является цепь НЕ. Она вьшолняет функцию, которая называется инверсией или отрицанием, и обычно называется инвертором. Цель инвертора - сделать состояние выхода противоположным состоянию входа. В логических цепях возможны два состояния - 1 и 0. Состояние 1 называют высоким, для указания, что напряжение в этом состоянии выше, чем в состоянии 0. Состояние О называют низким, для указания, что напряжение в этом состоянии ниже, чем в состоянии 1. Если 1, или высокое состояние, подано на вход инвертора, на выходе появится низкое состояние, или 0. Если на вход инвертора подать О, или низкое состояние, то на выходе появится высокое состояние, или 1. Работу инвертора отражает таблица на рис. 32-5. Вход инвертора обозначен А, а выход А (читается «не А»). Черточка над буквой А показывает отрицание А. Поскольку Рис. 32-5. Таблица истинности для инвертора. 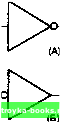 Рис. 32-6. Логические обозначения инвертора. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [ 166 ] [167] [168] [169] [170] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] [190] [191] [192] [193] [194] [195] [196] [197] [198] [199] [200] [201] [202] [203] [204] [205] [206] [207] [208] [209] [210] [211] 0.0014 |
||||||||||||||||||||||||||||||||||||||||||||