
 |
|
Главная Оптические магистрали [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [ 91 ] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] Рис. 10.7. Зависимость ю/* Uo(002-w)] (0,02-К))/* от W (шкицадь за- g.j штрихованного квадранта соответствует интегралу (10.2.34))  = 4447. При этом выявляется одна из характерных особенностей полупроводниковых лазеров: при высокой концентрации носителей тока могут быть получены очень большие коэффициенты усиления. 10.2.7. Полуэмпирическнй анализ Читатель, имеющий небольшую вычислительную машину и достаточно времени, может без особых трудностей обобщить эти результаты и получить зависимость коэффициента усиления от энергии фотона и плотности тока. Однако при этом имеет смысл учесть три обстоятельства, которыми мы пренебрегли: а) более сложный вид функций плотности состояний Sc и Sv, который учитывает хвосты зон при высокой концентрации примесей; б) полная функция распределения Ферми при ненулевых температурах; в) правила отбора, влияющие на вероятность переходов электронов между энергетическими состояния.ми в валентной зоне и зоне проводимости. Некоторые результаты такого анализа приведены на рис. 10.8 и и 10.9 Здесь было бы неуместным заниматься такими фундаментальными вопросами. Заинтересованный читатель может получить более подробную информацию из литературы: часть А [7.1], 110.1] или [10.2]. Из (10.2.25) ясно, что ключевым параметром, определяющим коэффициент усиления, является эффективная плотность тока: Ф = Лв„ут- - (10.2.36) Именно этот параметр представлен на рис. 10.8 и 10.9. Из приведенных на них зависимостей видно, что эффективная плотность тока должна быть достаточно большой для получения положительного значения коэффициента усиления. Величина и положение максимума коэффициента усиления определяют достижение лазерного порога и значение частоты генерации. Выше порога (Удф) усиление растет почти линейно с Уэф: гтах = Р!/эф-(Лф)о]. (10.2.37) с ростом температуры область положительных коэффициентов усиления распространяется на больший диапазон частот, но максимальная частота при этом снижается. Крутизна р зависимости gma от У„ф (10.2.37) обратно пропорциональна температуре. Это объясняется уши-рением распределения энергий носителей при повышении температуры. Изменение {Jyф)o с температурой примерно соответствует закону Т*/. Имеются теоретические предпосылки, основанные на упрощенной зонной структуре и показывающие, что пороговый ток растет пропорционально в компенсированном материале и - Т в сильно легированном материале. При дальнейшем анализе будем считать, что необходимое условие получения инверсной населенности и, следовательно, положительного коэффициента усиления заключается в том, что квазиуровень Ферми материала р-типа должен лежать в пределах зоны проводимости, т. е. Ерл-Ес. Обозначим через значение п, необходимое для удовлетворения такому требованию. Эта величина может быть получена в результате интегрирования распределения электронной концентрации п (ej) по всей зоне проводимости при условии, что ерл- = ее- Тогда п (ез) de., = Sc (82)2 (e2)de.„ (8.2.3), где Sc (ез) = Kc («2 - ec)/ при Kc == 2- lO* м-» - Дж-»/2 для GaAs и (е), определяемой выражением (10.2.1). Чтобы упростить математические преобразования, положим V = w/kT = (е„ - ее)/кТ = {е2-ер.\)/кТ. (10.2.38) Тогда интегрирование выражения (8.2.3) дает n, = Kc{kT) ? "Tw . =Кс{кТ)Еу1,{0). (10.2.39) J exp(v)-fl о Интеграл Ферми Ff (0) имеет значение 0,68. 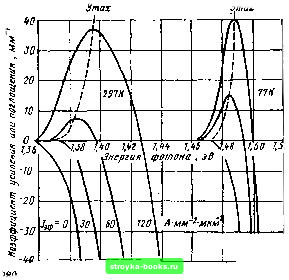 Рис. 10.8. Теоретическая зависимость коэффициента усиления в GaAs р-типа от энергии фотона /эф= = Т1внутМ А-мм-2 мкм-, концентрация акцепторов 4 10 м-) (F. Stern. Calculated spectral dependence of gain in excited GaAs,-.I. Appl. Phys 47, 5382-6 (1976).] Рнс. 10.9. Теоретическая зависимость максимального коэффициента усиления от /эф при различных температурах. (Расчеты учитывают хвосты зон и уменьшение ширины запрещенной зоны при концентрации акцепторов 4-10 м-. Стрелками указаны значения параметра (Лэф) при 77 и 297 К, см. (10.2.37).) [F. Stern. J. Appl. Phys. 47, 5382-6 (1976).] hO 5 30 i20
20 m 60 80 me , , Из (10.2.28) и (10.2.29) можно получить, что np~ = R,Jr=J,jer. (10.2.40) В сильно легированном материале можно считать р « Па- Тогда nJJerriA (10.2.41) (Лф)« = «л ет» = 0,68/СсЛл ern{kTf\ (10.2.42) В компенсированном материале р п, так что п-Лф/ег (10.2.43) (/,ф)„ ernl = ОЛт ег {kTf. (10.2.44) Результаты более сложных расчетов, приведенные на рис. 10.9, показывают, что значения Удф при 77 и 297 К соответствуют закону Т/. 10.3. ЛАЗЕРНЫЙ ПОРОГ Коэффициент усиления, необходимый для начала работы лазера, в соответствии с (10.1.18). g-2i>a = apacH----• (10.1.18) Этот результат, в принципе, можно применить и к полупроводниковому лазеру, подставив «/та вместо g. Однако следует более тщательно рассмотреть формирование лазерного резонатора в полупроводниковом лазере на двойной гетероструктуре. В силу высокого значения коэффициента усиления резонатор может быть сделан очень коротким по сравнению с лазерами других типов - порядка 0,2 ... 1,0 мм. Кроме того, коэффициент отражения зеркал не критичен и обычно оказывается достаточным френелевское отражение на границе раздела по- [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [ 91 ] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] 0.0013 |
||||||||||||||||||||||||||||||||