Используя формулу (6.1.20), можно затем упростить выражение (6.3.14) до вида

-=Л/о11-2А/. „(,,1 2А~1/2(---

\ (а-; 2) По

x2(l+6 + l)-)=/Voll-2Al-/2

(1-2А) +

2£(1+6)-- (а4-2) Л„ dw

==/V„ll--2Al-/2

I (a-!-2) /

(6.3.18)

Представив первый сомножитель в квадратных скобках в виде биномиального ряда, получим

5-«{l.f A + 13(A)V21 ...}

(а + 2)

1+ («-,-2-4-46) (3«-{-6-8-85) Д ,

(a + 2) 2(a + 2) -

1 (a-2-46) , (3a-2-86) (Д) (a f 2) (a 1-2) 2

(6.3.19)

Снова крайние группы мод соответствуют значениям = О и I !. Для значений а, удаленных от оптимального, их модовые группы будут такими, которые имеют самое длинное и самое короткое время распространения.

Тогда, ограничившись только членами первого порядка, находим

ДГ Ио - о

.„ Ja-2-46)

/ " (а 12)

(6.3.20)

Как и в предыдущем случае, минимум временной дисперсии имеет место при - tq, если пренебречь членами третьего порядка,

(а-2 -46) (а 12)

(За-2-86) Д2 Q («1-2) 2 ~

Отсюда

aU + ЗА/2) = 2(1 +26-4-(А/2) -6А],

а « 211 + 26-1- (А/2)] 11 + (ЗА/2)1-1« 2 [ 1 -- 26 + (А/2)1 х

X11 - (ЗА/2) +... I « 2 (1 + 26 - А) = (6-3.21)

в таком случае зависимость групповой задержки от параметра модовой группы I принимает вид

2Да (4 4 46 -6Л) Ла2

(4-; 46-2Д) (4 ; 46- 2Д) 2

оАЧ (6.3.22)

Здесь пренебрегли членами с б и А ио сравнению с 1. Выражение (6.3.22) достигает своего максимума при 1/2, когда

(to-- Q - ATmin No imsc. (6.3.23)

Отсюда видно, что наличие материальной дисперсии оказывает двойное влияние на межмодовую дисперсию в градиентных волокнах с а-профилем: приводит к появлению индекса Ло группы мод в формуле (6.3.23) для минимума модовой дисперсии и изменяет оптимальное значение а (формула (6.3.21)), требуемое для достижения этого минимума модовой дисперсии, иа величину, которая зависит от б, а следовательно, и oTdA/dk.

Напомним, что здесь не была учтена внутримодовая дисперсия: эффекты уширення импульса, обусловленные влиянием материальной и волноводной дисперсий для каждой моды. Этот вопрос будет рассмотрен в следующем параграфе.

Осущестатение лишь одного легирования материала сердцевины волокна для получения желаемого профиля показателя преломления обычно приводит к нежелательным изменениям дисперсионных свойств стекла вдоль радиуса. Вот почему величина А может стать функцией длины волны. (Так же, как и значение величины а, что уже было учтено при нашем анализе.) Эти эффекты, обусловленные свойствами материала, могут быть скомпенсированы путем управления профилем по-казателя преломления, т. е. изменением а. Если а меньше 2, моды более высоких порядков (более наклонные лучи) распространяются быстрее, чем моды низших порядков (осевые лучи). Это может компенсировать разницу показателей преломления между сердцевиной и оболочкой, которая увеличивается с увешчением длины волны. Если же а больше 2, быстрее будут распространяться аксиальные лучи, и это может компенсировать величину А, которая уменьшается с увеличением длины волны. В результате оптимальное значение а зависит от выбора материала примесей, используемых для получения требуемого изменения показателя преломления, и от длины, волны, на которой должно работать волокно. Значения функции б (К) для различных легирующих примесей можно определить по известным дисперсионным характеристикам, рассмотренным в § 2.2.2. Затем их можно использовать для нахождения оптимальных значений а на различных днинах волн. Результаты приведены на рис. 6.6.

Разработчик оптического волокна имеет в своем распоряжении целый ряд легирующих примесей, которые позволят управлять профи-

лем показателя преломления градиентного волокна и его дисперсионными свойствами, если эти примеси использовать в различных сочетаниях. Более глубокий анализ показал, что в очень широком диапазоне профилей волокна возможно уменьшить межмодовую дисперсию до минимального значения

с [1-(1- 2Д)/П

при Л 1.

(6.3.24)

Эта теория применима для всех волокон, имеющих цилиндрическую симметрию и изготовленных из однородных материалов. Если материальная дисперсия не изменяется, оптимальный профиль волокна определяется однозначно. В самом деле, если материальная дисперсия постоянна по сечению сердцевины волокна, как и было принято в только что рассмотренной теории, то оптимальный профиль волокна - это а-профиль, причем значение а определяется формулой (6.3.21). С другой стороны, возможен и произвольный выбор проф1:ля показателя преломления, однако в таком случае изменение материальной дисперсии {dnidk) по сечению сердцевины волокна должно происходить в строгом соответствии с требованиями критерия минимума мдовой дисперсии. Если осуществимо управление характеристиками материальной дисперсии стекла (т. е. ве.;ичиной dndk и производными более высоких порядков), то становится возможным поддерживать минимум дисперсии в диапазоне длин волн.

Были высказаны предположения, что при еще более тщательном профилировании показателя преломления сердцевины могли бы быть получены даже меньшие значения межмодовой дисперсии, чем предсказываемые выражением (6.3.23). Вероятно, это представляет больше теоретический интерес, нежели имеет практическое значение. Более вероятно, что необходимость создания сверхширокопо" лосных оптических линий связи будет удовлетворена за счет использования одиомодовых, а не градиентных волокон, которые требуют тщательного контроля и управления их параметрами при изготовлении. В любом случае необходимо использовать лазерные узкополосные источники излучения, чтобы минимизи-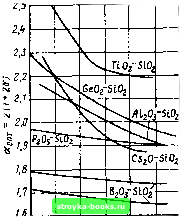

0,5 0,6 0.1 0,8 0,9 1,0 7,1

Л,МММ

Рис. 6.6. Зависимость оптимальных значений а от длины волны. [Данные получены нз нитерферен-циоиных измерений, выполненных Н. М. Presby and I. P. Kaminov.- Appl. Optics 15, 3029-36 (1976).]

Значения atom были определены no дисперсионным параметрам 6(К) с помощью формулы (6.3.21) прн Л=0. Предполагалось, что оболочка сделана нз чистого кварца