и, наконец

я -

(1-2А-/2 1-2А-1-1 + А+--(А)-!- ...\\\-

(а 1-2) 4Д5

= 1 +

{« ; 2)

2) д I (За-2) (А)2

(а ! 2)

-+...

(6.3.7)

Крайние модовые группы характери,зуются q - 2 ч q Q (т. е. 5л;0и~1)иих время распространения определяется формулами

ctjria / « 1 * (6.3.8)

«о

(а 1-2)

(а -2) 2

Эти модовые группы содержат моды с самыми быстрыми и самыми медленными скоростями распространения, за исключением случая волокон, у которых значение а лежит в области 2. в таком случае модо-вая дисперсия представляет собой просто разность между /„ и tq. в первом приближении она будет равна

(6.3.9)

При а > 2 модовые группы более высоких порядков распространяются медленнее, чем группы низких порядков и волокно оказывается недокомпенсированным по отношению к дисперсии. Если же а < 2, справедлива обратная картина и волокно становится перекомпенсированным. в действительности минимум дисперсии имеет место при значении а несколько меньше 2, когда tg и tq имеют одинаковое значение, а промежуточные модовые группы распространяются более быстро. Этот эффект иллюстрирует рис. 6.4. Таким образом, условие минимума дисперсии имеет вид

t,=tQ. (6.3.10)

На основании этого можно написать

1 = 1 +

(а-2)

(За -2) Д2

(a-f-2) (а-2а-4-+-(За -2) А = 0,

4-[ 2Л

2(1 +

2-1-зл

(6.3.11) 1&5

Подставив найденные значения а в формулы (6.3.11) и (6.3.7), получим

(to~Q =

(4-2Д)

1(1-1).

(4-6Д) Д2

(4 -2Л) 2

(6.3.12)

Разумеется, полученная разность во времени распространения моды самого низкого порядка и q-к модовой группы будет равна нулю при I О и I 1 и будет достигать максимума при 1/2, когда

(6.3.13)

Нахождение оптимальных значений а позволяет таким образом оказывать значительное влияние на модовую дисперсию в градиентном волокне. Сравнение гюлученного выражения с (2.1.8) показывает, что дисперсия в градиентном волокне уменьшается до (Д.8) части дисперсии ступенчатого волокна, имеющего одинаковые значения л„ и А. Рассмотрим волокно, у которого Пд 1,5, а Д = 0,01. В случае ступенчатого волокна дисперсия приблизительно будет равна АТП -

Недономпемсировамнвеу волонно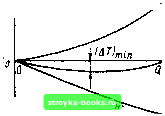

Переномпенсирова мае волонно

Рис. 6.4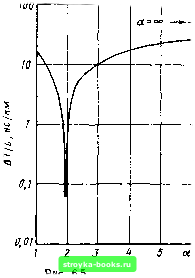

Рис. 6.4. Зависимость времени распространения tq от номера модовой группы ц для перекомпенсированиого и иедокомпеисироваииого волокна с а-профилем

Рис. 6.5. Зависимость межмодовой дисперсии от параметра профиля пока.чателя преломления а в пренебрежении материальной дисперсией (кривая построена для волокна, имеющего по=1.5 н Д=0,01)

ПоА/с=50 нс/км. В случае же градиентного волокна с а-профилем, имеющего те же значения «о " А. при а = 2(1 - А) = 1,98 модовая дисперсия составила бы всего А7 = (пА/с) (А/8) 62,5 пс/км. При этом произведение полосы пропускания на расстояние было бы равно около 8 ГГц- км, т. е. увеличилось бы почти на три порядка. На рис. 6.5 приведена кривая теоретической зависимости межмодовой дисперсии от а для градиентного волокна, которая позволяет высказать следующие два соображения: 1) чтобы гюлучить минимум дисперсии, необходимо очень тщательно управлять значением а; 2) всякое изменение показателя преломления, которое приближает профиль волокна к параболическому, приводит к существенному уменьи!ению межмодовой дисперсии в нем.

6.3.2. Межмодовая дисперсия с учетом материальной дисперсии

Попытаемся найти оптимальный профиль показателя преломления волокна с учетом дисперсионных свойств материала его сердцевины. Это означает, что необходимо учесть зависимость от частоты величин По, А и Q, входящих в выражение (6.1.40). Приводимое ниже рассмотрение просто повторяет только что сделанное выше для среды без дисперсии, однако математические выкладки становятся существенно более громоздкими. Как и ранее,

р, = Ро11-2Д£!/2. (6.3.14)

Однако теперь

Ji-= i = JEiLi 1 2Д/2-р„ 11-2А-/2 (а-iL J-I / йы dw \ dw do),

= Зц 1 2 А]/2 - iblil 11 2 А j -1/2 (А+ I j. с с \ d(o do) /

Введем обозначение

.-.:з(Ал„«)~«/(«+2), (6.3.15)

где к2 - параметр, не зависящий от частоты со. Тогда do) \а + 2 / Ango) do) "

= ( z:\ I-/а.2ло(о/Уо-«о« -V (6.3.16)

\a-h2/ Лп§ 0)2 \ » " " d(e /

Учитывая, что = d {п(л)1й(л

do) где

gJo м Яр А, dA (6 1.20)

==(z2:-\lsA.2{\ + b), (6.3.17)

V а + 2 / п„ о)