Рис. 5.10. Графики зависимости нормализованного параметра распространения bkm от параметра нормализованной частоты V для некоторых самых низких мод в ступенчатом волокне в случае использовании приближения слабо направляющего волокна.

[Взято из статьи D. Globe. Weakly guiding fibers. Appl. Optics 10, 2252-2258 (1971).]

на с помощью мод высоких порядков, которые далеки от своих частот отсечки. В этом случае можно упростить описание характеристик мод, если воспользоваться приближенным представлением функций Бесселя при больших аргументах (х > 1)

УЛ)«(2/ял:)/2со5[х-(А:я/2) -(я/4)1. (5.3.10) Условие отсечки при этом принимает вид

Л ,(«„а) = 0. (5.3.11)

Таким образом, при ит а > 1 оно преобразуется к виду

cos [Uft„ a-ikn/2) + (Я/4Я = 0. (5.3.12)

откуда следует

ита-(кл/2) + Ш) ===m + -Ly (5.3.13)

Ukma= -lk+2m+-Ly

(5.3.14) 135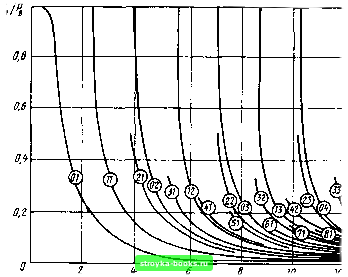

Рис. 5.11. Графики зависимости относительной доли мощности моды, распространяющейся в оболочке, от параметра нормализованной частоты V-(Взято из статьи D. Globe. Weakly duiding fibers. Appl. Optics 10. 2252-2258 (197I).J

Хотя выражение (5.3.14) выведено из условия отсечки, однако полное изменение произведения Ukm а в пределах всех возможных частот ограничено значением, несколько меньшим л, поэтому относительное изменение ит будет очень малым в условиях принятой аппроксимации, а именно при (fe + 1/л + 1/2) > 1. Это означает, что все моды с одинаковым значением (fe + 2т) становятся приближенно вырожденными. Следовательно, разумно их идентифицировать с помощью нового целого числа модовой группы q ~ k + 2т. В таком случае

и,„адл/2. (5.3.15)

Приблизительно {q/2) пар значений (fe, т) создает одно и то же значение д, при этом каждой нз (fe, т) пар соответствуют четыре моды. Таким образом существует 2q мод, связанных с каждой модовой группой q. Постоянная распространения этих мод может быть получена в нормализованном виде либо подстановкой (5.3.15) в (5.3.9)

km J 2l£l

либо В ЯВНОМ виде из (5.2.2)

(5.3.16)

(5.3.17)

Наибольшее допустимое значение для q имеет место при р, = р. Обозначим это максимальное значение квантованного числа модовой группы буквой Q. Тогда

Р=-Р1 = Р!-. (5.3.18) Откуда следует

Q* = (Pf-PI)-. (5.3.19) л

и, наконец, воспользовавшись (5.2.16), находим

Q = 2У/л. (5.3.20)

Когда V велико, что должно быть справедливым в рассматриваемом случае, общее число М мод порядка (к, т), которые могут распространяться в волокне, приближенно определяется соотношением

М= У (2(7) «Q*. (5.3.21)

Несколько лучшее приближение дает формула

М « nqm. (5.3.22)

Воспользовавшись формулой (5.3.20), получим

М iliPl -f 4- J {п\~-п1) = 2я (.VЛ) (5,3.23)

где А г - площадь сердцевины, а Л/Л, как и ранее, числовая апертура волокна. Данное соотношение не яапяется неожиданным, поскольку квадрат числовой апертуры определяет оптическую мощность, которая может быть введена в волокно, число распространяющихся в нем мод, если все они возбуждаются одинаково, а также полную мощность, которая может распространяться по волокну.

Чтобы вычислить значение М для типичного многомодового ступенчатого волокна, примем л, = 1,46, = 1,45 и 2а 50 мкм. В таком случае (ЛЛ) =-- 0,17. При длине волны источника 0,85 мкм получаем V - 31,5, число модовых групп Q 20, а общее число мод, распространяющихся в волокне и определяемое формулой (5.3.23), .-М ж 500.

S.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ

Представленные на рис. 5.6 и 5.7 зависимости дают возможность увидеть различные причины, вызывающие расширение оптического импульса при его передаче по волокну. В §2.2.3 было установлено, что время распространения оптического сигнала при прохождении пути длиной / равно

t = vg = / (dp/d(o). (2.2.36)