Уравнение (П3.9) легко проинтегрировать, если разложить второе слагаемое и умножить на г. Это приводит к следующему соотношению:

2„. А. 4 - 4- (пг ) - о. ,ПЗ. .3)

ds ds ds ds ds ds \ ds j

Таким образом, величина nr {d(f/ds) также постоянная, значение которой зависит только от того, каким образом луч входит в волокно. Следовательно,

ds dz ds dz

где, как показано иа рис. П3.2,

--- --го5ес7о(со»РоС<)-чфо -со5ао«1пфо). (П3.15>

\ dz Jz= О

Параметр / иногда называют угловым моментом луча.

Рис. П3.2. К доказательству соотношения (П3.15):

а-луч входит в волокно в точке Р(го, Фо. 0) и после прохождения вдоль оси расстояния dz достигает точки Q(ro+dr, фо + ф, dz). Таким образом,

PQ~ds, PR dz.ds cos у„ (ПЗ.И)

6) вид вдоль оси волокна: если RS\ \ TQ\ \ UV, RT-RU-TU Sq- (гodг)dф,

однако

dscos Po. откуда следует

RU - - ds cos Po cos фо. Аналогично

QV ----- dscos «0, откуда получаем

ти ds cos «0 sin Фо,

(Го -l-iir) dKf - ds (cos Po cos фо - cos «о sin фо). Так как {dr/r„) -»-0,

cos Pj cos фо - cos «0 si n Фо.

Следовательно,

/ =:r Гр sec Yo (со5РоС05фо -coswosin фо). (ПЗ. 15)

На основании (П3.8) можно получить дифференциальное уравнение для r(z) следующим образом. Заметим, что если воспользоваться выражениями (П3.12) и (П3.14). то соответственно

dr dz

dz ds

dr E

dz n

(П3.16)

d(p ds

Следовательно, уравнение (П3.8) преобразуется к виду

I Е п -

dr dz

т. е.

£

dr \

,2 £2

dn dr

ds \ dz / nr dr

Однако имеет место соотношение

d- г dz dr

ds [ dz )

E n

(П3.17)

dz- ds dz

Поэтому, подставив (П3,19) в (П3.18) и поделив иа Р/п, окончательно dn

dr dz

£2 dr

f 1 d „ P d / 1 \

r ~ 2£2 dr 2 dr \r- У

(П3.18)

(П3.19) получим (П3.20)

П3,1. РЕШЕНИЯ УРАВНЕНИЙ ТРАЕКТОРИИ ЛУЧА

Уравнения (П3.20), (П3.14) и (П3.12) определяют траектории каждого луча, входящего в градиентное волокно. Чтобы получить выражения в более явной форме, умножим сначала все члены уравнения (П3,20) на 2 (dr/dz):

dr tPr d I dr V- 1 d dr

dz dz- dz [ dz j ~ £2 dr " dz ~

d f \ \ dr Id . d

£2 dz

(n2)-/2.

{П3.21)

Непосредственное интегрирование полученного дифференциального уравнения дает

dr \2 /.2

£2

-\-А.

(П3.22)

Значение постоянной интегрирования А определяем из начальных условий:

dr \2 «2 12

\ dz /г= О новка выр:

£2 rl

Подстановка выражений (П3.!2) и (П3.15) дает 478

+ г1

• 1,

(П3.23)

{П3.24)

поскольку

Таким образом, получаем

Пусть Tl и Гг есть корпи уравнения

(П3.25)

(П3.26)

Эти корни являются функциями профили ггоказателя преломления п (г) и исходной траектории луча, что выражается параметрами Е и / (рис. ПЗ.З). Если оба корня действительные, радиусы rj и Га соответствуют точкам изгиба траектории, в которых dridz - О и относительно которых траектория луча симметрична. Поэтому положение луча по радиусу имеет периодическую зависимость от г, как это показано на рис. П3.4. Расстояние вдоль осн волокна Zq. равное пространственному периоду.

/2 \l/2

(П3.27)

£2

Здесь быго использовано выражение (П3.25).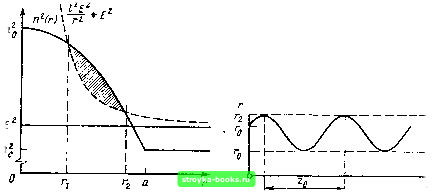

Рис. П.3.3

Рис. П.3.4

Рис. ПЗ.З. Графики функций п(г), и {lEjry+E, образующих область, ограниченную г и г2 для случая, когда уравнение (П3.26) имеет действительные корни.

Очевидно соответствие рис. 6.2, а

Рис. П3.4. Периодическая зависимость радиального положения луча от расстояния вдоль оси