
 |
|
Главная Оптические магистрали [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [ 128 ] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] 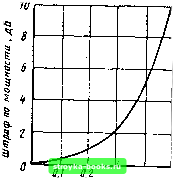 да на «хвостах» оказывается больше, чем это обычно следует из рачета. Это не влияет на среднеквадрэтические значения, однако вызывает значительные различия в расчетных уровнях взаимных помех между символами и, таким образом, приводит к завышенному значению штрафа по мощности. В [14.5] были вычислены значения для принимаемых импульсов различной формы. На рис. 15.12 приведены результаты для гауссовых импульсов. Данная кривая чрезвычайно важна, поскольку она показывает возможность обмена между скоростью передачи данных и мощностью сигнала и, следовательно, связывает между собой эффекты затухания и дисперсии в оптическом волокне. Можно видеть, что плата за шум ие превышает 1 дБ, если а остается менее Т/5. Однако штраф по мощности резко увеличивается, если длительность импульса превысит эти значения. Таким образом, совершенно ясно, что на практике характеристики системы связи обычно ограничены либо дисперсией оптического волокна (ограниченная полоса пропускания), либо затуханием в волокне (ограниченная мощность). Для встречающихся в практических системах связи форм импульсов условие того, что штраф по мощности не превышает 1 дБ, может быть смягчено до а (~ т/2) <Г/4, причем оно более или менее независимо от формы импульса. 0,3 0,t а/т Рас. 15.12. Зависимость штрафа по мощности от среднеквадратической длительности импульса для импульсов гауосовской формы 15.4,4. Изменения уровня мощности: модовый шум Во всех представленных до сих пор вычислениях предполагалось, что мощность падающего на фотодетектор оптического сигнала описывается детерминированной функцией времени и нет причин для ее статистических изменений. Кроме того, принималось, что наблюдаемый при детектировании света дробовой шум полностью обусловлен статистической природой процесса детектирования квантов. Это предположение несомненно потребует некоторого дальнейшего толкования при пересмотре механизмов эмиссии в источнике излучения. В действительности определяемая (12.6.1) и (14.2.1) амплитуда дробового шума представляет собой минимальный уровень. Имеется несколько процессов, которые могут заставить зависящий от сигнала шум превысить это значение и учесть распределение, отличное от пуассоновского (15.2.2). Некоторые из процессов связаны с источником излучения, другие -с передачей сигнала по волокну и, наконец, третьи - со статистическими характеристиками процесса детектирования. Можно представить совершенный источник излучения, который излучает непрерывную волну с постоянной амплитудой и частотой, скорее похожей на несущее колебание, излучаемое радиопередатчиком. Примером может служить излучение на выходе стабилизированного по-частоте одномодового лазера. Чтобы эту волиу можно было использовать лля целей связи, ее следует «нарезать» на короткие импульсы (например, с помощью фотозатвора), длительность которых велика по сравнению с периодом оптических колебаний, но мала по сравнению с интервалом, в пределах которого волна сохраняет неизменную фазу. Этот интервал называют временем когерентности т; он является важным параметром оптического излучения. Следует ожидать, что такое излучение, упав на фотодиод, создает на его выходе определенный уровень дробового шума. Рассмотрим оптическое излучение, создаваемое обычным некоге-рентиым источником. Такое излучение рассматривается как последовательность независимых элементарных актов испускания атомами фотонов, происходящих в случайные моменты. Предположим, что это излучение испытывает частые случайные изменения фазы. Следовательно, отсутствует какая-либо фазовая корреляция в течение длительных периодов и хотя в данном случае время когерентности Те остается большим по сравнению с оптическим периодом, оно будет малым по сравнению с типичным временем передачи сигнала или временем отклика любого обычного фотодетектора. Таким образом, (1 ) « Те « Т. (15.4.2) В этой ситуации случайные изменения в процессе излучения усредняются за время отклика фотодетектора и снова наблюдается обычный уровень дробового шума, определяемый (12.6.1). Для излучения таких источников существует непосредственная связь между шириной спектральной линии и временем когерентности. Это соотношение имеет вид: где у = ДШ = Д /-относительная ширина спектральной линии излучения источника, определенная в гл. 2. Иногда бывает удобно определять расстояние вдоль направления распространения, на протяжении которого излучение остается синфазным как длину когерентности 1с- Следовательно, 4=-£-t„=-JL . (15.4.4) где п - показатель преломления. Если принять у = 0,03, что характерно для таких некогерентных источников излучения, используемых в оптической связи, как свето- диоды, то соответствующее значение времени когерентности, например Тс •= 0,1 ПС, подтверждает выполнимость условия (15.4.2). Следовательно, с достаточным основанием можно полагать, что приводимый в этой главе статистический анализ применим как к лазерным, так и к светодиодным источникам излучения. Имеются некоторые данные о существовании избыточного шума, генерируемого в самом источнике излучения, в частности, в лазерах, на частотах, близких к частотам собственного резонанса. Однако еще не ясно, ведет ли это к существенному ухудп1ению результирующих характеристик оптических систем связи. Имеет место значительно более сьезный эффект, который связан с линией передачи и наблюдается при использовании узкотюлосных лазерных источников излучения в сочетании с многомодовым оптическим волокном. Он стал известен как модальный шум. Обычно когерентное излучение лазера возбуждает в многомодовом волокне ряд мод распространения. Пока сохраняется их относительная когерентность, наблюдаемая на конце волокна, картина излучения принимает вид известной спекл-структуры, порождаемой лазерным излучением. Она является результато.м конструктивной и деструктивной интерференции, наблюдаемой в любой заданной плоскости. Пример спекл-структуры изображен на рис. 15.13. После прохождения достаточно большого расстояния межмодовая дисперсия вызовет появление относительных задержек между различными модами, превосходящими по величине время когерентности света в каждой моде. Когда это случится, спекл-картина исчезнет в однородном излучении фона. Появление спекл-картины само по себе не является достаточным условием для возникновения модального шума. Для его появтения необходимо выполнение следующих двух требований: в линии передачи должна быть точка, где осуществляется селекция мод, причем перед  Рнс. 15.13. Картина поля излучения б ближней зоне, создаваемая когерентным светом, распространяющимся в многомодовом волокне. {Взято нз книги С. Р. Sandbank (ed) Optical Fiber Communication Systems. John Wiley (1980) @, STL Ltd.] Число спеклов приблизительно соответствует числу распространяющихся мод. Диаметр сердцевины волокна 50 мкм [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [ 128 ] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] 0.0013 |