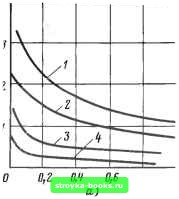0,В t,c

Рис. 2.7. Вольт-секундные и джоуль-секундные характеристики бетэловых резисторов .

а - вольт-секундная характеристика для проводимостей резистивного материала {i -10" Ом"* м~*; 2 - 4-10" Ом~м"; 3 - 1,0 Ом~м~; 4 -10 Ом м б - джоуль-секундная характеристика для проводимостей резистивного материала {1 - 0,04 Ом~-м~; 2 - 0,1 Ом~-м~; 3 - 0,2 Ом~м~; 4-\Оы м ,5-10Ом м")

от адиабатического процесса нагрева РЭ, связанного с накоплением тепловой энергии, к квазиустановившемуся теплрвому режиму, когда на распределение температуры в изделии оказывают влияние условия теплоотдачи.

Детальная проработка конструкции требует в свою очередь расчета распределений напряженности электрического поля, температур в элементах конструкции резистора с помощью решения системы дифференциальных уравнений в частных производных.

Предполагается построение моделей по крайней мере трех уровней.

Первый уровень математических моделей основан на решении систем уравнений, подробно описьшающих физические процессы, протекающие в изделии. Кроме того, в эти модели могут быть включены эмпирические формулы, полученные на основе обобщения экспериментального материала, например формулы для пробивных напряжений. Модели первого уровня используются для поверочных расчетов и могут частично заменить этапы изготовления опытных образцов и их испьпания. Заметим, что в большинстве случаев математическое моделирование (естественно, в разумных пределах) позволяет существенно сократить цикл проектирования, так как изготовление макетных образцов часто связано с длительными трудоемкими процессами.

Изготовление опытных образцов каждого нового конструктивного варианта влечет за собой повторение всего комплекса трудоемких тех-

нологических процессов. Кроме того, достаточно трудно планировать число циклов проектирования, а следовательно, и загрузку подразделений предприятий, изготовляющих опытные образцы.

Проектирование с использованием таких моделей не предполагает полного отказа от изготовления и испытаний опытных образцов. Результаты испытаний опытных образцов используются для корректировки математических моделей, описывающих различные процессы в изделиях.

Математические модели второго уровня создаются на основе математических моделей первого уровня с помощью аппроксимации. Модели второго уровня менее точны, чем первого, зато гораздо менее трудоемки. Эти модели используются на этапе выбора рациональных технических рещений и при многовариантных расчетах, производимых для анализа влияния изменения технологических параметров процесса производства на качество изделия. Построение такого рода моделей существенно связано с классом проектируемых изделий. Действительно, силовые резисторы представляют собой ненастраиваемые устройства, поэтому для обеспечения приемлемого выхода годных необходимо, чтобы зависимость выходных параметров и критериев качества от входных параметров была достаточно "пологой, плавной", чтобы в условиях производства обеспечить приемлемый выход годных при случайных вариациях входных параметров.

Будем считать, что для математических моделей вьшолняется условие Липщица

Я(р) -Я(ро) < lollp-Polloo, кроме того, для их градиентов имеет место неравенство

llgradЯ(р) - gradЯ(ро) IIi < Li IIр - Ро И . где р, Ро G suppll, Lq, Li - константы,

IIP-PO lloo = sup Ip-Pob

p, po G supp П

allp-polle = S (jP/t-PoH ) к =1

Рассмотрим вариацию Я(р), если р изменяется в многомерном параллелепипеде [р, р]. Пусть с =0,5 (р + р), d = (р - р), тогда

Я(р) G [ Я(С) - ~ lid lloo , Я(С) -Ь lid lloo ].

Используя неравенство для градиентов, получаем для верхней границы функции в интервале [р, р] 28

L1

Я(р) < Я(с) + <£га(1Я(с), р-с>+ - 11р-с11оо,

где {*,*) - скалярное произведение в нрюстранстве параметров.

Оценивая скалярное произведение через норму градиента, получаем

Я(р) < Я(с) + ~ 11Ега(1Я(с)111 lldlloo +--lldlloc.

Аналогивдо Для нижней границы

llgraa/(c) 111 lldlloo -

Я(р) > Я(с) - - 11Егас1Я(с) lli lldlloo - - lid lie

Д)1я получения границ изменения функции объединим неравенства:

Я(р) G [Я(с)---lldllocmin (1оЛвгас1Я(с)111 +

+ ili idlioo); 2

1 L , Я(с) + - lid Иоо max (Lo, llgrad Я(с) II1 + -lid lU).

(2.14)

Полученное неравенство может быть использовано для оценки моделей, когда носитель пространства параметров покрыт семейством параллелепипедов, а в центре каждого параллелепипеда произведена оценка выходного параметра и его градиента.

Индуктивная интерполяция (ИИ). Еще одним методом извлечения информации о значениях параметров проектируемого изделия является .использование опыта предшествующих разработок и представляет собой отображение

Пвых = ИИ(Пвх. »,{ Пр}), (2.15)

где Пвх Пвых ~ нечеткие описания входных и выходных параметров; { Пр} - описание прототипов проектируемого изделия; St - структура изделия, т.е. граф, определяющий зависимость выходных параметров от входных.

Отметим, что в (2.15) не требуется явное описание математической модели функционирования, информация о выходных параметрах проектируемого объекта извлекается индуктивно (на основе примеров аналогичных разработок), отсюда и название метода - метод индуктивной интерполяции. На рис. 2.8 проиллюстрирован случай, когда пространство как входных, так и выходных параметров двумерно, множество прототипов объекта, представляющее собой базу интерполяции, состоит из трех элементов.