Граничным значениям вектора критериев качества J, J будут соответствовать граничные значения вектора конструктивных параметров. Таким образом, решая исходную и сопряженную задачу расчета теплового режима силового резистора, получаем заодно и линейную аппроксимацию нечеткого множества критериев. Для более точного восстановления (3) необходимо использовать покрытие пространства критериев.

Перейдем к постановке задачи оптимизации в условиях неопределенности. Введем нечеткое множество параметрических (q) и критериальных (q) ограничений. Допустимость нечеткого решения q определяется результирующим нечетким множеством, являющимся пересечением

5л (q) = j-n (q) Тк (q) J-q (q) Тз (J (q))•

Задача оптимизации сводится к определению четкого вектора конструктивных параметров

q* = Argmax (min (Mn(q). f (q). /aCq). /y(q)))-

<?

Эта задача в свою очередь может быть решена методами математического программирования.

Расчет повторно-кратковременных режимов работы силовых резисторов. При проектировании резисторов, предназначенных для работы в импульсных и повторно-кратковременных режимах, приходится сталкиваться с задачами расчета циклических режимов. К этим задачам относятся расчеты неустановившихся тепловых режимов, когда периоды нагрузки мощностью W- длительностью Ti скачкообразно сменяются нагрузками V/. и Т2 - Времена нагрузки т- и пауз Гг постоянные. Температура силового резистора от одного периода к другому возрастает, но не достигает установившегося циклического режима, когда максимумы и минимумы температуры в начале и в конце каждого периода будут постоянны. Решение подобных задач необходимо для определения числа допустимых повторных включений силового резистора под нагрузку в энергосистемах с автоматическим повторным включением.

При работе резисторов в промьпдленных установках для управления повторяющимися технологическими процессами актуален расчет периодических тепловых режимов. В этом случае максимумы и минимумы температуры в начале и конце интервалов времени rj + Г2 являются постоянными.

Обычным подходом к решению задач расчета тепловых режимов при периодической нагрузке является интегрирование систем нелинейных дифференциальных уравнений. Данный метод целесообразен для расчета неустановившихся режимов. Однако при расчете периодических режимов, когда постоянные времени элементов схемы заме-96

щения различаются на несколько порядков, а период, прилагаемый к резистору нагрузки, сравним с минимальной постоянной времени, интегрирование приходатся проводить на сотнях и тысячах периодов, что приводит к недопустимо большим вычислительным затратам и погрешностям получаемых результатов. /

Объем вычислений значительно сокращается, если для решения указанной задачи использовать подход, базирующийся на применении вариации решения основной задачи [37]. Суть метода нахождения периодического решения задачи (2.68) сводится к следующему: требуется решить краевую задачу (2.68) с условиями

Т(0) = Т(игп), (2.92)

где - период приложения нагрузки; п - целое число, п>1.

Основная система дифференциальных уравнений, описьшающих переходный процесс, решается на временном отрезке Тц=Т1 + rj, и на каждой итерации вычисляется невязка 11Т(0) - Т(иг)11, далее определяется градиент невязки по начальным условиям Т(0) и периоду Гр. Указанные данные используются для минимизации невязки одним из градиентных методов, приводимым в [19]. Решение краевой задачи (2.68) с условием (2.92) эквивалентно, как отмечалось выше, мини-мизащш

У= liT(O)-Т(игп)11 (2.93)

по вектору начальных условий Т(0) и периоду rjj-

Значение / на г-й итерации можно вычислить, решив систему (2.68) с начальным условием Т (0) = Тр на временном отрезке [О, игр,]. Как и ранее, вьмислим линейную часть вариации (2.93) в окрестное-ти Т:

6/ = 2[бт(ип) - «Sn(GiT(«-n) +W3)]x

x [Т(0)-Т(«тп)]. (2.94)

В то же время линейная часть вариации может быть вычислена по (2.79).

Применение данного метода подразумевает решение системы дифференциальных уравнений с использованием матричной экспоненты. Развитие метода, снимающего данное ограничение, изложено в [37].

При помощи рассмотренной выше методики расчета нестационарных и периодических режимов был произведен анализ термической стойкости резистора типа РБОН-3.

На рис. 2.36 приведен график зависимости максимальной температуры от времени приложения импульса нагрузки, причем для длительности импульса нагрузки Ti = 0,05 с при стандартных испытаниях и максимальном превышении температуры резистора 95 К и температу-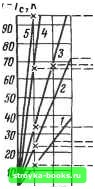

о 0,05 0,1 Та,с О ш гчо 3S0 т воо гго

Рис. 2.36. Нестационарные тепловые режимы резистора РБОН-3 для различны.х мощностей и длительностей приложения нагрузки;

1- W=\ МВт; 2-2 МВт; 5-3 МВт; 4-6 МВт; J - 9 МВт

ре окружающей среды 308 К мощность, прилагаемая к резистору, равна 9 МВт. Заметим, что линейная зависимость температуры от времени указывает на адиабатический характер теплового режима.

Повторное включение резистора возможно только в том случае, если максимальная температура при повторном включении не превышает допустимой. Приняв в качестве допустимой Тдоп =403 К, проведем расчеты зависимости числа включений от скважности импульсов (рис. 2.37, а) и прикладьшаемой мощности (рис. 2.37, б). На ЭВМ моделировался стандартный режим нагружения резистора мощностью 3 МВт с чередованием импульсов нагрузки ri = 0,05 с и пауз в приведенной ниже последовательности:

г, - 0,3 - т, - 900 - Ti - 0,3 - г, - 1800 - т, - 0,3 - т, -

- 900 - г, -0,3 - т, -7200 - п - 900 -т- 0,3.

Время пауз здесь дается в секундах. Зависимость максимальной температуры в резисторе приведена на рис. 2.38- Очевидно, что максимальное превьш1ение температуры резистора, равное 92 К, приходится на четвертый импульс нагрузки и не превосходит допустимого превышения температуры.

При многократном нагружении резистора мощностью 3 МВт с длительностью импульса Ti = 0,05 с резистор выходит на периодический режим ({жс. 2.39). Разработанная методика использовалась и для расчета на ЭВМ тепловых режимов резисторов, шунтирующих высоковольтные вьислючатели типа РБШН. Бьшо определено максималь-