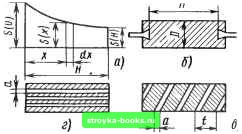Рис. 2.17. Резисгивные элементы непроволочных резисторов, допускающие вычисление их сопротивлений с помощью непосредственного интегрирования:

а - плоский РЭ с незначительным изменением ширины; б - объемный РЭ; в - тонкослойный РЭ; г - тонкослойный РЭ с продольной нарезкой; д - тонкослойный РЭ со спиральной нарезкой

Сопротивление тонкослойного РЭ цилиндрической формы

R = а~ А"» H/D,

где h - толщина резистивной пленки.

Для юстировки резисторов, а также увеличения его сопротивления резистивный слой может быть прорезан рядом продольных изолирующих прорезей (рис. 2.17, г). Сопротивление РЭ связано с числом прорезей Nil их шириной а соотношением

Я/)Г (f- fl)

Таким образом, сопротивление резистора может быть увеличено не более чем в 2-3 раза. Значительного увеличения сопротивления можно достигнуть с помощью спиральной нарезки (рис. 2.17, д). Сопротивление РЭ со спиральной нарезкой определяется шагом нарезки t, шириной прорези а:

R=a- А"»

TiDt (f- fl)

Аналогично может быть определено сопротивление и проволочных резисторов с однослойной намоткой. Рассмотрим порядок приближенного расчета проволочных резисторов [22]. Определим площадь каркаса РЭ S из условия обеспечения заданной допустимой температуры РЭ Гд„„:

S = /[(Гдоп - Тс)а].

где W - мощность, рассеиваемая резистором; Тс - температура среды; а - приведенный коэффициент теплоотдачи, который в естественных условиях лежит в пределах 5 - 10 Вт/ (м К).

По площади каркаса и удельному сопротивлению резистивного материала выбираем диаметр проволоки, мм:

d = 0,011 (5а" /?" A:")/

где о - электрическая проводимость проволоки, Ом"-м"; 5 - площадь каркаса, м; к ~ коэффициент, численно равный отнощению щага намотки к диаметру проволоки. Дня РЭ, наматьюаемых изолированной проволокой, /: = 1,05 1,2.

Вычисленный диаметр проволоки следует округлить до ближайще-го стандартного размера, определяемого ГОСТ для выбранной марки проволоки. Далее рассчитаем длину провода, пользуясь соотнощением

/р = тг - 10" a?d

где d - диаметр проволоки, мм; R - сопротивление РЭ, Ом; /р - длина резистивного провода, м.

При расчете резисторов с многослойной обмоткой следует иметь в виду, что коэффициент теплоотдачи при ее использовании уменьшается по сравнению с однослойной обмоткой в 2-3 раза. Порядок расчета РЭ при этом несколько меняется [22]. Вначале определяется длина каркаса

Н = у/S/ink г).

где kl = 0,33-0,67.

По гаощади каркаса 5 и длине Н вычисляется наружный диаметр обмотки

=S/ttH.

Чтобы исключить сползание обмотки с каркаса, наружный диаметр принимается несколько большим, чем наружный диаметр обмотки. Внутренний диаметр d выбирается из условий механической прочности каркаса. После выбора марки обмоточного провода определяется его диаметр, мм:

. » 6.67

V kl R а

где 2 - коэффициент заполнения, равный 1,1-1,4.

Вычисленный диаметр приводится к стандартному размеру, и рассчитьшается средняя длина одного витка провода многослойной обмотки

ср = - ~--•

в свою очередь длина провода определяется но формуле /р = 47г/?2 а,

а по длине провода и средней длине витка определяется число витков

Расчет распределения электрического поля РЭ методом граничных элементов. Как было показано, непосредственно определить сопротивление можно только для весьма ограниченного класса РЭ. Для точного расчета распределения потенциала в РЭ, напряженностей электрического поля, энергии, сопротивления необходимо либо решать краевую задачу (2-31), (2.33), либо минимизировать функционал (2.43).

Основными требованиями, предъявляемыми к численным методам, являются Возможность проводить расчеты электрических характеристик РЭ произвольной конфигурации на ЭВМ без перепрограммирования для каждого типа РЭ; простота ввода данных о конфигурации РЭ, о краевых условиях. Указанным требованиям удовлетворяют методы конечных и граничных элементов. Сущность первого метода сводится к тому, что тело РЭ разбивается на ряд конечных элементов простой формы: треугольников в двумерном случае и тетраэдров в трехмерном. В каждом конечном элементе потенциал аппроксимируется линейной функцией координат *.

Вне данного конечного элемента эта функция понимается равной нулю. При этом распределение потенциала внутри конечного элемента однозначно выражается через потенциалы в его вершинах. Далее конечно-элементная аппроксимация потенциала подставляется в функционал (2.43), который в свою очередь минимизируется по значениям потенциалов в вершинах конечных элементов. На контактах фиксируется значение потенциала; на непроводящих границах, где плотность тока, нормальная к ним, равна нулю, никаких ограничений на потенциал не накладывается. Можно показать, что конечно-элементая аппроксимация приводит к необходимости решения задачи минимизации квадратичного функционала энергии [17]

Э = min (и П, U+ Пг и) (2.48)

*Существуют многочисленные варианты метода конечных элементов, использующие более сложные конфигурации конечных элементов, включая криволинейные, а также полиномиальные аппроксимации потенциала степени вьпле первой [25].