Отметим, что при постоянной приложенной нагрузке в РЭ может идти переходный процесс, связанный с распределением температуры. Более того, изменение злектрофизических параметров резистивных материалов может пртводить к перераспределению нагрузки в нем. Однако характерные времена переходных процессов тепловых режимов силовых резисторов многократно превышают времена для злек-тромагнитных переходных процессов в непроволочных силовых резисторах, позтому при проведении расчетов тишовых режимов распределение вьщеляющихся мощностей в РЭ в каждый момент времени можно считать постоянным.

2.4. РАСЧЕТ РАСПРЕДЕЛЕНИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ В РЕЗИСТИВНЫХ ЭЛЕМЕНТАХ СИЛОВЫХ РЕЗИСТОРОВ

Распределение злектрического поля в силовых резисторах зависит от конфигурации его РЭ, неподвижных контактов, злектрофизических свойств используемых резистивных материалов. В свою очередь распределение электрического поля в РЭ определяет его сопротивление и мощность, в нем выделяющуюся. Если форма РЭ отличается от цилиндрической или прямоугольной, то непосредственное вычисление распределения электрического поля в РЭ и сопротивления может вызвать трудности.

В настоящем параграфе рассмотрим уравнение, описывающее распределение потенциала в РЭ, методы его решения и расчета сопротивления.

Распределение потенциала в резистивном элементе. Распределение потенциала в проводящей среде описьшается уравнением [17]

V(a(x, E)vu(x)) =0, (2.31)

где а - электрическая проводимость резистивного материала, зависящая в общем случае от пространственных координат х и напряженности Е; V - оператор набла; ум = + + к-- ; i,j, к -

единичные направляющие векторы, соответствующие осям координат

Х1,Х2,Хз.

Когда электрическая проводимость резистивного маюриала не зависит ни от пространственных координат, ни от потенциала, (2.31) переходит в уравнение Лапласа

Ам(х) =0, (2.32)

где Д - оператор Лапласа.

Считая контакты РЭ идеальными, можно поставить следующую краевую задачу для определения потенциала м: мр = О на одном из контактов, мр = f/ на втором контакте, плотность тока через непроводя-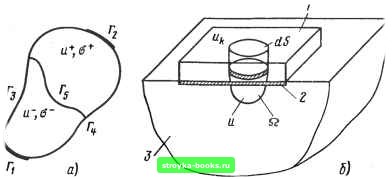

Рис. 2.16. Резистивные элементы:

а - с идеальными контактами; б - с неидеальными контактами; 1 - контакт; 2 - переходный слой; 3 - резистивный материал

щую часть границы равна нулю (рис. 2.16, д) :

= 0,

(2.33)

где Эм/Эи - частная производная, нормальная к границе.-

Если электрическая проводимость резистивного материала внутри РЭ меняется скачком, то на такой внутренней границе имеют место условия

Ъи-

""1Г5 = "*1Г5

(2.34)

означающие, что на внутренней границе потенциалы равны, кроме того, плотность тока, протекающего нормально к границе, не испытьтает скачка (м", а~, и*, а* - потенциал и электрическая проводимость с одной и другой сторон границы соответственно).

Резистивные элементы с кусочно-постоянным изменением проводн-МОС1И. Резистивные элементы с кусочно-постоянным по координатам изменением проводимости являются характерными для силовых резисторов. Дня них нелинейное уравнение (2.31) с помощью преобразования Кирхгофа можно свести к линейному [25]. Пусть в некоторой части РЭ электрическая проводимость не зависит от координат, тогда уравнение (2.31) запишется в виде

V(a(M) vm) = 0.

Сделаем замену переменной ip={dip/du, Vu).

Принимая dif/du = а(и), получаем из уравнения для распределения потенциала в РЭ

Ap(x) =0,

в свою очередь

. ip{u) = J o(u)du, "о

(2.35)

где щ - произвольная постоянная.

Таким образом, задача о распределении потенциала в кусочно-постоянной по координатам нелинейной среде может быть сведена к ли-нейнол уравнению Лапласа (2.35). Краевые условия (2.32) и (2.33) могут быть преобразованы следующим образом:

"о "о

dip

= 0.

Несколько сложнее обстоит дело на внутренней границе Fs- Введем \р (if) - преобразование, обратное преобразованию Кирхгофа, так что \р (ip) =и. Тогда на границе Fj имеем

i-iF =If,;

(2.36)

Таким образом, преобразование Кирхгофа позволяет в ряде случаев свести нелинейную задачу к линейной.

Вольт-амперные характеристики силовых резисторов с РЭ, выполненными на основе электропроводящего бетона (бетэла), имеют вид [11]

(м-мо) = Ло/",

(2.37)

где и - напряжение, приложенное к резистору; / - ток; Ro - коэффициент пропорциональности; а - коэффициент нелинейности, принимающий значения в диапазоне а =0,7 -i-1.

Вольт-амперная характеристика (2.37) легко может быть преобразована к виду

а(м-«о) = ао(м-«о)-/" Соответственно