(геометрически это эквивалентно представлению уровневых множеств многомерными параллелепипедами) позволяет сократить трудоемкость алгоритма и сделать ее линейной по размерности пространства и числу элементов базы интерполяции. Кроме того, имеет место вложенность уровневых множеств результатов интерполяции при увеличении степени принадлежности; реэупьтат индуктивной интерполяции элемента базы совпадает с ним самим.

Математические модели, использующие ИИ, позволяют уже на этапе проектирования получить информацию, которую принципиально невозможно получить другими методами, например, о стабильности параметров изделий, так как испытания сравнимы по времени со сроками разработки изделия или даже превьппают их, отсюда информация об указанных параметрах может быть извлечена искнючитеньно из опыта разработки изделий-аналогов.

Другой вариант алгоритма ИИ рассмотрен в [12].

Расчет выходных параметров изделия в условиях неопределенности. Перейдем к расчету выходных параметров конструкции, когда все или часть входных параметров заданы нечеткими значениями, на универсальном множестве параметров { П}. Расчет выходных параметров предполагает отображение нечеткого множества у(Рвх) заданного на универсальном множестве входных параметров, на нечеткое множество ?вых (Рвых) заданное на универсальном множестве выходных параметров { Пх}; {П} = { П Ib"{ Пх }> где х -знак декартова произведения.

Отображение осуществляется с помощью оператора Н

{nbix} =Я({Пвх}),

где { Пвых } ~ образ входного множества при отображении Я, {Пвых} {ПвыхЬ Функция принадлежности д, вычисляется с помощью принципа обобщения [4] : ""

"вых

= <

max тш(/1дзх(Рвх),Мя(РвхРвых))

Рвых -(Рвх)

о в противном случае.

(2.21)

В данном случае дувх интерпретируется как желательность (возможность) того, что входные параметры принимают четкое значение Рвх представляет собой совместимость значения выходных параметров Рвых значениями входных параметров pg.

Функция принадлежности Mg-gx связана с нечетким множеством х(Рвх)"я - с оператором Я.

3-6319

в частности, если все значения входных параметров допустимы, ц. = 1, а для обычного четкого отображения имеет место тождество {Iff = 1.

Рассмотрим построение ых ™ входным данным 5" и оператору Н. Когда носитель множества 1? конечен и состоит из небольшого числа элементов, построение <?"вых помощью непосредственных вычислений не представляет сложности. Однако, если suppSx имеет мощность континиума и он многомерен, вычисление ых может бьггь сведено к процедуре моделирования. В отличие от вероятностного рассматриваемый тип моделирования может быть назван возможностным, так как он сводится к вычислению не вероятности, а возможности того, что выходной параметр принимает заданное значение. Как и раньше, будем предполагать, что вектор выходных параметров представляет собой "плавные, пологие" функции вектора входных параметров с ограниченными вариациями в { Пх} Будем считать, что на носитепе пространства входных параметров виррПвх имеется покрытие, причем каждый элемент покрытия связан со значением входного параметра { рх}/- свою очередь покрытие носителя пространства входных параметров индуцирует более или менее равномерное покрытие области { Пх} • Для каждого элемента покрытия можно вычислить степень принадлежности для /-го элемента покрытия выходного параметра по формуле

*вых (Рвых/) = mln(,зx (Рвх/) Мя(Рвх/ Рвых/))-

Границы вариагщи выходного параметра на элементе разбиения могут быть оценены по (2.14). Случай одномерных { Пх } и { Пдх 1 проиллюстрирован на рис. 2.9. Заметим, что в отличие от вероятностного моделирования каждое значение функции принадлежности покрытия представляет собой нижнюю оценку функгщи принадлежности выходных параметров, а при монотонности Н совпадает с ней. Мно-гоэкстремальность Я порождает несколько ветвей гвых (Рвых) (" рис. 2-9 показано штриховой линией). Вьщеление единственной ветви осуществляется с помощью операгщи взятия максимума. Отметим еще одну особенность возможностного моделирования. В отличие от вероятностного моделирования функция принадлежности не нормирована к единице

{Пвых }

Отметим, что даже при использовании моделей второго уровня трудоемкость многовариантных расчетов технического решения достаточно велика. Это заставляет искать методы, позволяющие сократить объем вычислений за счет, во-первых, сведения нечетких задач к набору интервальных задач и использования интервального анализа [13], во-вторых, вьщеления особых классов задач. 34

Рис. 2.9. Расчет функции принадлежности для выходного параметра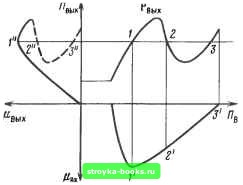

Рассмотрим случай, когда уровневые множества Увх(д) и УвыхСд) представляют собой многомерные интервалы, т.е. отсутствует взаимодействие входных и выходных параметров между собой. Вычисление выходных параметров можно осуществить как по (2.21) с помощью принципа обобщения [4], так и путем применения функции Я к каждому из уровневых множеств Увх(д)- Получившиеся многомерные интервалы Увых (м) могут быть слиты в нечеткое множество

•вых (Рвх)-

В общем случае использование интервальных методов позволяет получить верхнюю оценку по включению для ?"gj,ix (Рвх) Пусть { / } -множество интервалов на числовой прямой R. Интервал /д. G { / } будем представлять в виде [дд-, Ьд-]. Арифметические операции на интервале { / } введем следующим образом [13] :

h* 12 = [fli *bi, а2 *b2] =

= [miniai * bi, ai * Ьг, 02* bi, 02 * bi),

mxiOi * bi, Oi * b2, 02 * bi, 02 * b2)],

где * - операция из множества четырех арифметических действий.

При делении интервал [02, Ьг] не должен содержать 0. Заметим, что вычитание не является операцией, обратной сложению, а деление -умножению.

Действительно

[2,4] - [1,2] = [0,3]; [0,3] -Ь [1,2] = [1,5];

[1, 4] / [1, 2] = [О, 5, 4, 0]; [О, 5, 4, 0] х [1, 2] = [О, 5; 8,0].

В интервальной арифметике результат может зависеть от способа вычисления выражений:

[-1,1] x ([2,1] - [1,0])= [-1,1] x [2,0] = [-2,2].