
 |
|
Главная Длительная эволюция [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [ 25 ] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] ниже примере строятся графики первых четырех полиномов Чебышева первого рода: ChebyshevT[0, х] - полинома нулевого порядка, равного тождественно единице, ChebyshevT[l,i] = х, а также полиномов ChebyshevT[2,a;], ChebyshevT[3,a;] (рис. 3.3): р13 = Plot[Evaluate[Table[ChebyshevT[n,x], {п,0,3}]], {х,-1,1}, PlotStyle- Table[{Thickness[0.003+2i 10-3]},{i,0,3}]]; 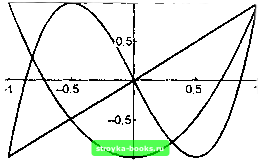 Рис. 3.3 Рассмотрим теперь остальные из семи специфических для функции Plot опций: AxesOrigin, Compiled, GridLines, MaxBend, PlotDivision, PlotPoints, PlotStyle. Опция GridLines, установленная на Automatic, вызывает появление на рисунке сетки вертикальных и горизонтальных прямых, исходящих из точек координатных осей с координатными отметками. Эта сетка видна на графике р11, приведенном выше. Опция PlotStyle совпадает с опциями AxesStyle и FrameStyle, но определяет графический стиль представления вычерчиваемых линий. Адаптивный алгоритм, которому следует „Математика" при построении графиков, предусматривает получение достаточно гладких кривых. Одним из критериев гладкости является величина угла между последовательными отрезками пря- мых, аппроксимирующих кривую между соседними точками, в которых вычисляются значения функций, задающих кривую. Величина этого угла устанавливается опцией MaxBend, по умолчанию он равен 10°. Количество точек, в которых производятся вычисления, регулируется опцией PlotPoints, которая, если не оговорено иное, равна 25. Если угол между последовательными сегментами превосходит значение опции MaxBend, то производится дробление интервала между соседними точками, но таких шагов дробления не может быть больше, чем значение опции PlotDivision. Для уменьшения времени вычисления функций в выбранных по адаптивному алгоритму точках производится их компилирование, заключающееся в создании некоторого псевдокода. Однако последний может привести к уменьшению точности вычислений. Если нужно избежать подобной потери точности, то следует прибегнуть к опции Compiled -¥ False. Функция ParametricPlot позволяет рисовать кривые и семейства кривых, заданных параметрически. Ее описание с соответствующими изменениями совпадает с описанием функции Plot, в частности она имеет те же опции. Мы ограничимся поэтому простым примером применения этой функции (рис. 3.4): р14 = ParametricPlot[{Cos[t],Sin[3t]},{t,0,2Pi}, PlotLabel -4 "Lissajou figure"] Lissajou figure 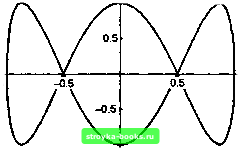 Функция ListPlot предназначена для графического представления дискретных численных данных и имеет своим первым аргументом либо список вида datal={yi,y2,•••Уп}, либо список вида data2={{a;i,yi},{i2,y2}f{2;n.yn}}, либо список данных создается какой-либо функцией, например Table. В первом случае будет графически представлена совокупность точек с координатами (г,у;), во втором - с координатами (ii,yi). Пусть массив данных data3 имеет вид: data3 = {1., 1.18785,0.81045,0.09574,-0.41614,-0.51789, -0.49499, -0.60536, -0.65364, -0.28532,0.42549, 0.95922,0.96017} Ниже следует его графическое представление (рис. 3.5): ListPlot[data3, PlotStyle -> {Pointsize[0.04]}] 0.5 - -0.5 Рис. 3,5 Следует обратить внимание, что графическая директива, управляющая размером точек, не Thickness, как это было в случае линий, а PointSize. Функция ListPlot имеет дополнительные опции AxesOrigin, GridLines, Plot Joined, PlotStyle. С помощью PlotJoined -> True точки на графике будут соединены отрезками прямых линий (рис. 3.6): [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [ 25 ] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] 0.001 |